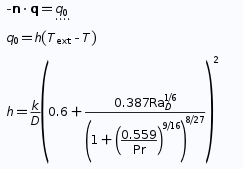타 사이트에서 간단한 열유동 test를 위해 컴퓨터 케이스 cad를 구하다 simple한 문제에 대해 test요청을 받아 한 테스트 결과입니다.
그 사이트에도 올렸지만 실제 해석이 그리 어려운 케이스는 아니고, 어디 보여주기도 뭣한 케이스지만, 간단히 보시기에 재미있으실 듯 하여 여기도 올립니다.
1. 문제의 정의
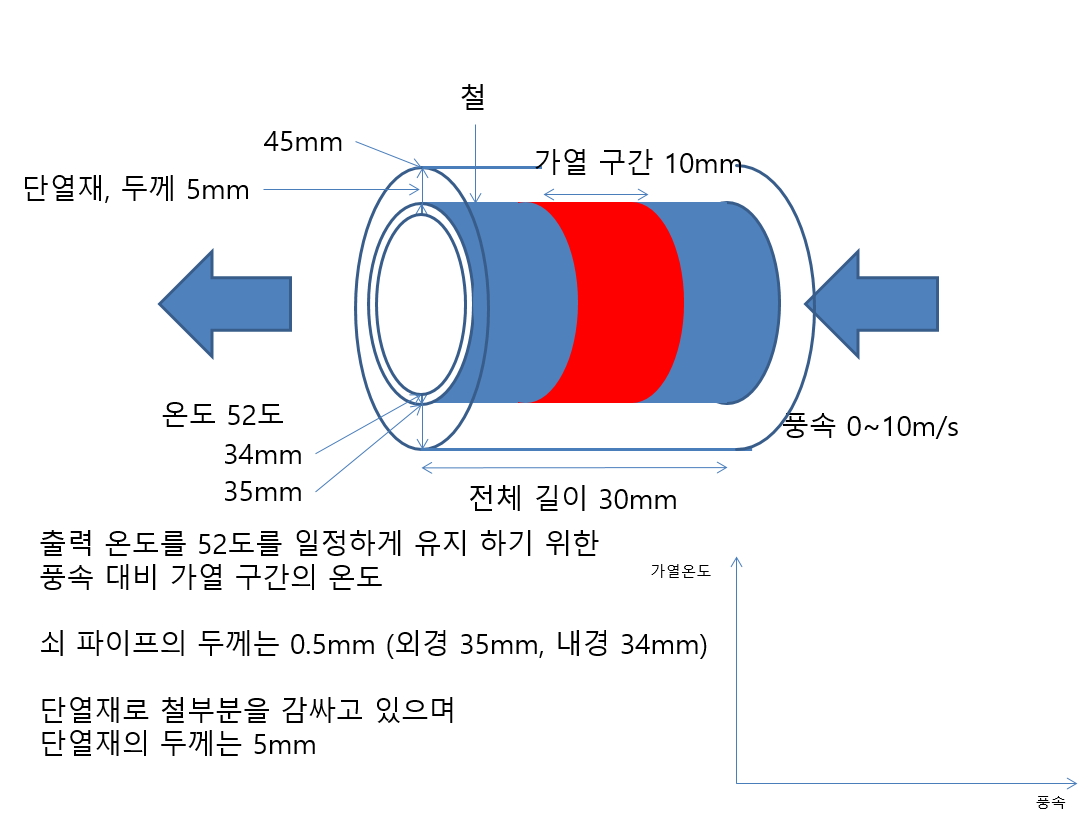
요청한 Test는 하기 그림과 같습니다.
드라이기의 코일 대신 외벽을 가열시키고, 풍속을 0~10m/s로 증가시킬 경우 출구쪽에서의 온도 52도를 유지하기 위해서 지정된 벽면(빨간색)에서는 어떤 온도를 부여해야하는가? 에 대한 요청이었습니다. (아래 그림 참조)
2. 해석 설정을 위한 조건들
2.1 사용된 물성치
2.1.1. 철 : Steel AISI 4340 (Heat Capacity, 475(J/kg*K), Density 7850(kg/m^3), Thermal conductivity 44.5(W/m*K)-등방성)
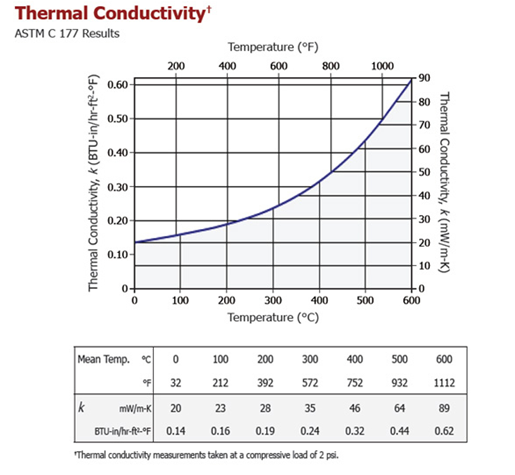
2.1.2. 단열재 : 에어로젤 (Heat Capacity, 2.2(J/kg*K), Density 1900(g/m^3), Thermal conductivity 제공해주신 온도에 따른함수)
2.1.3. 유체 : 공기, 유체의 경우 역시 사용하는 툴에서 정의된 물성치를 사용하였습니다. Heat capacity와 Dynamic viscosity, thermal conductivity의 경우 온도에 대한 함수로 구성되어 있으며, Density는 온도와 압력에 대한 함수, Specific heat ratio의 경우 1.4를 사용하였습니다.
2.2 해석의 물리조건
이 경우 중심축을 회전 축으로 놓으면 축대칭이 됨으로, simple한 테스트로써 2D 축대침 모델을 짰습니다.
2.2.1 열전달
열전달 구속조건으로는 우선전도, 대류를 포함하였으며, 복사는 제외시켰습니다.
사실 이 같은 문제에서 만일 온도가 1000도까지 필요하다고 가정할 시 복사에 의한 열전달도 무시할 수 없는 수준으로 올라가겠지만, 심플 테스트이고, 온도가 그 수백도 이하구간에서 52도를 나타낼 것이라고 예상하였기 때문에 제외하였습니다. (온도차가 수백도를 넘어 수천도 이상이 될 경우에는 오히려 대류에 비해 수식상 복사가 훨씬 큰 영향을 주게될 것 같습니다)
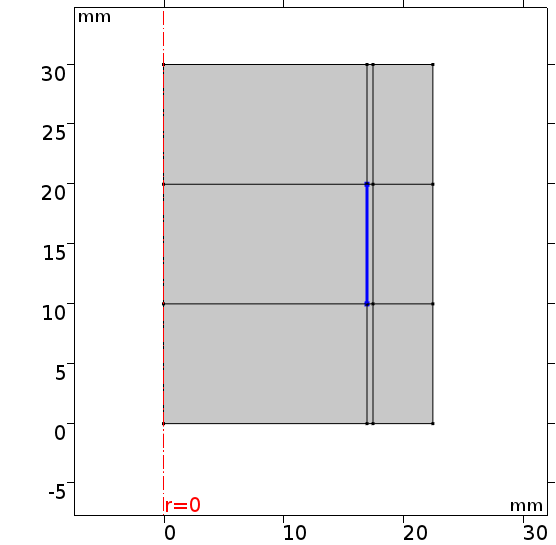
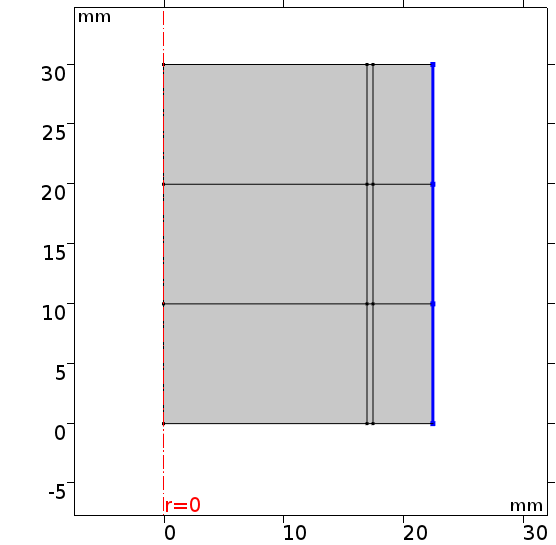
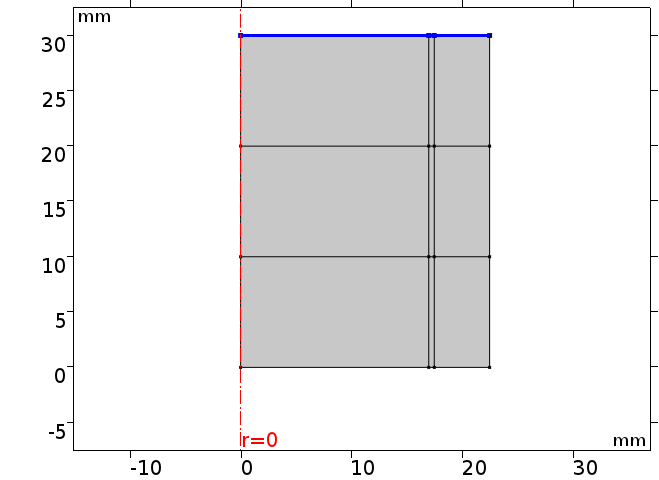
구속조건으로는 하기 그림과 같이 파란 색의 외벽에서 온도 변화를 주었습니다.
또한 외벽의 경우 공기와 닿아 있는 부분이기 때문에 실린더 옆면에서 일어나는 natural convection에 의한 flux 조건을 주었습니다. 이 때 외부 온도는 1기압에 20도 조건을 주었을 떄로 계산하였으며 정확한 수식은 하기에 첨부하였습니다.
들어오는 유체의 온도 역시 20도를 부여하였으며, 그 외 조건은 축대칭 조건 및 단열조건으로 처리하였습니다.
사실 보다 상세한 해석을 위해서는 더욱 많은 조건들(단열재 및 철의 위아래 부분 등에 대한 처리 등)을 사용해야 하나
이럴 경우 시간이 많이 걸릴 수 있고, 현재는 단순화된 Test를 수행하는 해석이기 때문에 이러한 부분은 오차 범위 내로 생각하고 생략합니다.
2.2.2 유체
유체의 경우 층류 유동으로 해석하였습니다.
사실 유체조건의 경우 특별히 어려운 조건은 존재하지 않습니다.
유입(inlet)및 출구(outlet)조건만 설정해 주면 끝입니다.
다만 유체와 열을 연동할 경우, 열에 의한 밀도변화가 발생할 것이고, 이 부분에 대한 압축성만 고려해 주었습니다.
2.2.3 연동
열 해석 및 유체 해석을 one-way가 아닌 two-way형식으로 하여 두 물리조건이 상호연동하여 해석하도록 하였습니다.
2.3테스트 케이스
우선 본 테스트의 경우 일반적으로 optimization을 시켜도 되나, 다수 케으스를 돌리는 것이 설정 면에서 편하기 떄문에
온도를 100도~ 1000도까지 증가시키며 총 10개의 case * 속도를 0.1m/s와 2m/s부터 10m/s까지 2간격으로 증가시킨 6개의 case에 대한 해석을 수행하여 총 60개의 case 스터디를 진행하였습니다.
속도의 경우 0을 넣지 않은 이유는 단순 열전달에 의한 열전달만 볼 시 0m/s에서는 stationary 상태까지 도달하는데 시간도 많이 걸릴 뿐더러 단순 열에의한 대류현상만 고려됨으로 이는 제외하였습니다.
또한, 이 경우 해석의 목적 자체가 평균온도가 출구에서 52도가 되는 구속조건을 찾는 것이기 때문에 그 과정을 나타내는 과도해석(time-dependent)이 아닌 충분한 시간이 지난 후 평형상태에 도달하여 시간흐름에 관계없이 안정된 해를 찾는 정상상태(stationary) 해석을 수행하였습니다.
3. 해석 결과
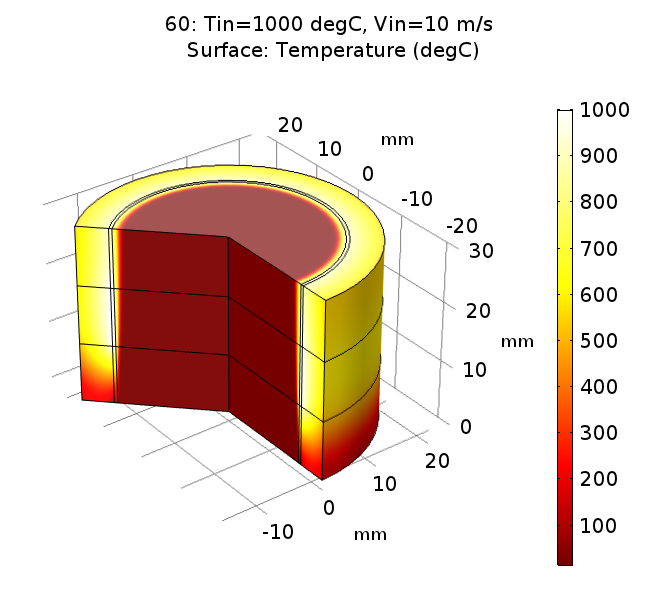
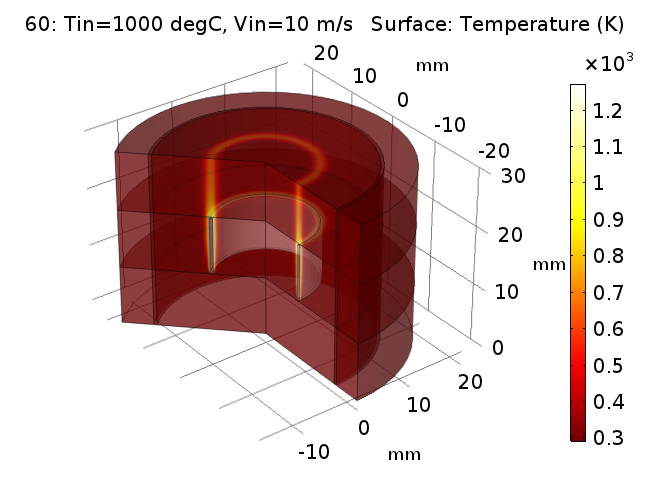
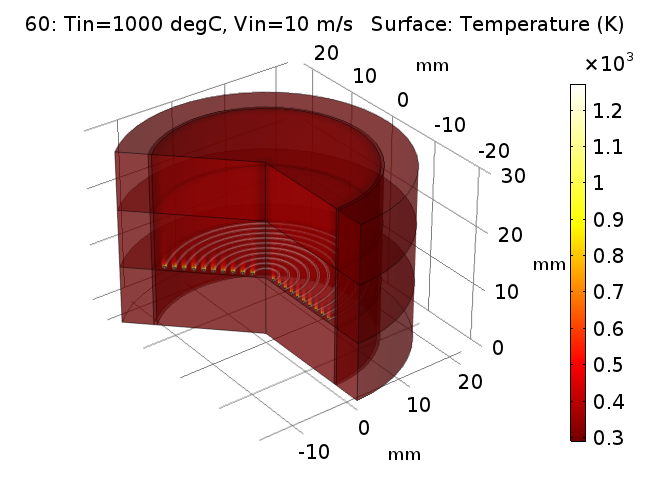
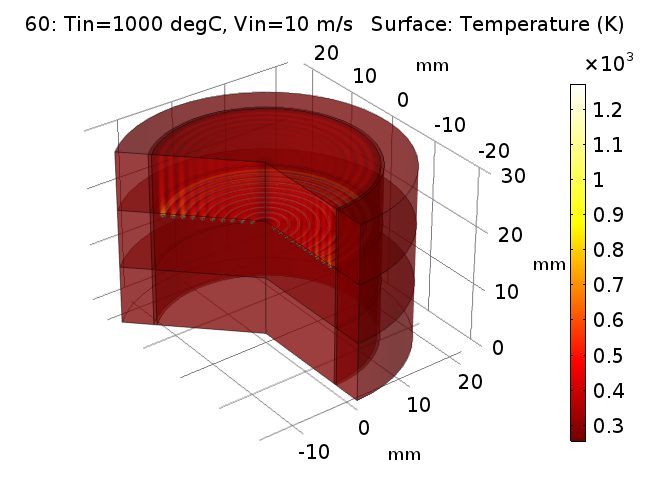
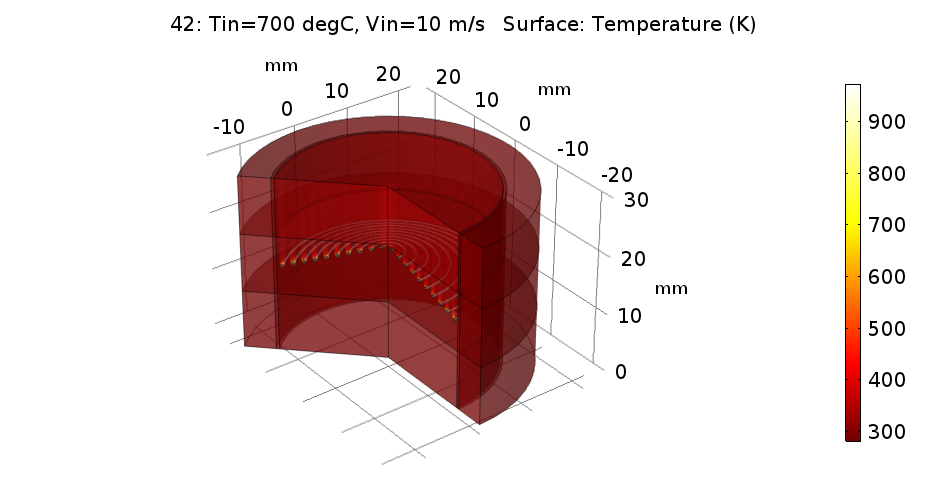
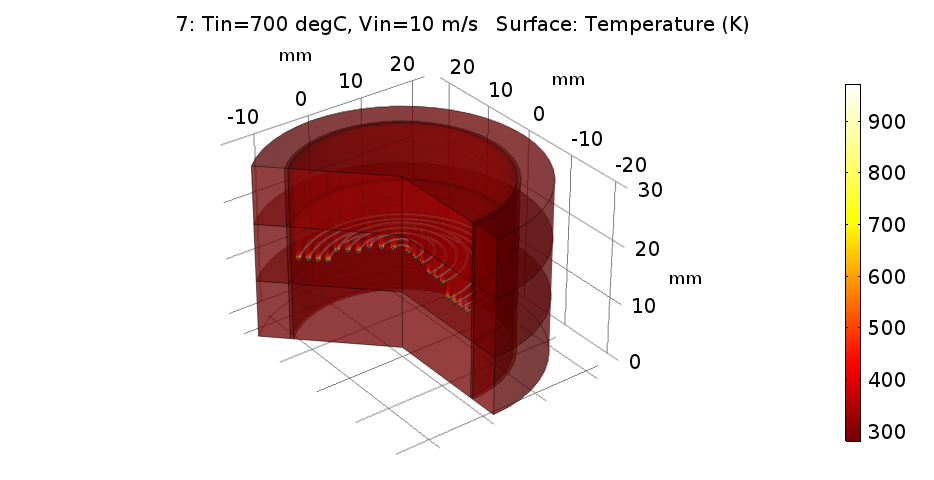
궁금해 하시는 해석 결과입니다. 총 60개의 결과가 존재하기 떄문에 우선 최종적인 결과 중 마지막 케이스(1000도, 10m/s)에 대한 3차원 결과를 보여드립니다.
사실 이런 테스트에서는 상기 그림과 같은 형태는 크게 중요하지 않습니다.(하지만 있어보이죠)
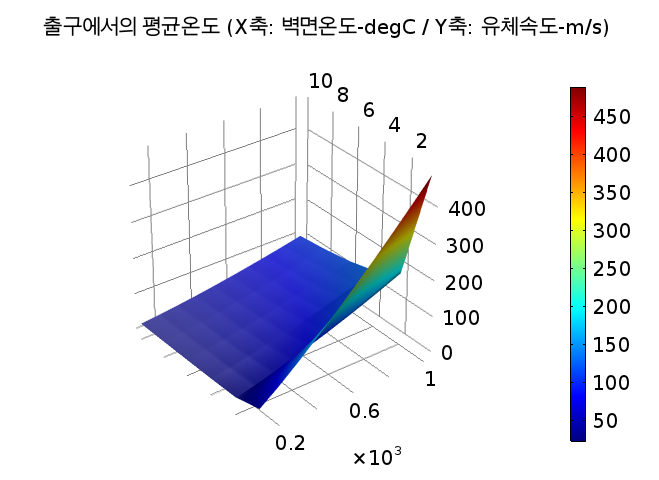
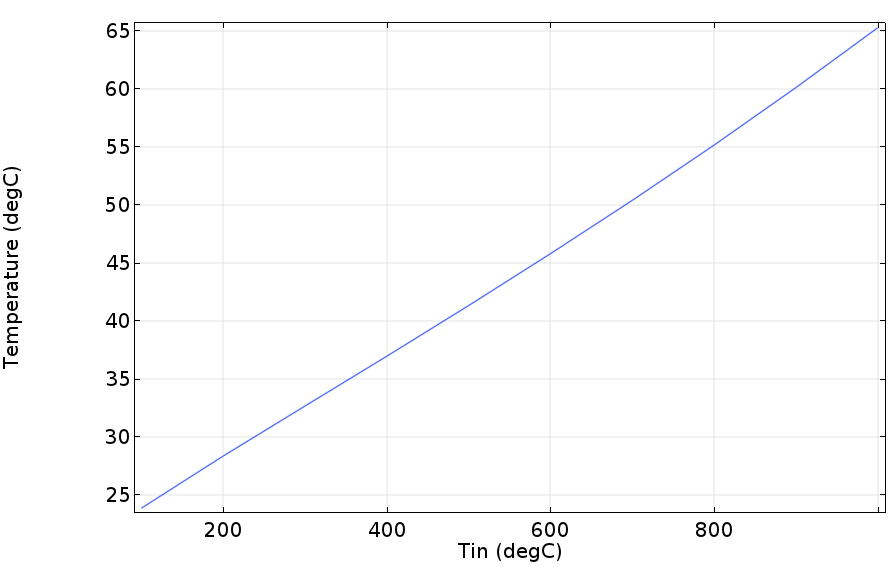
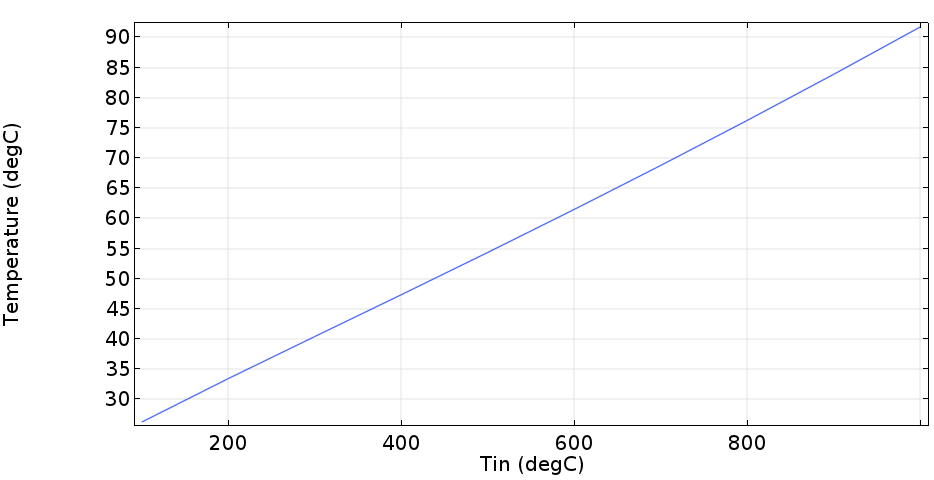
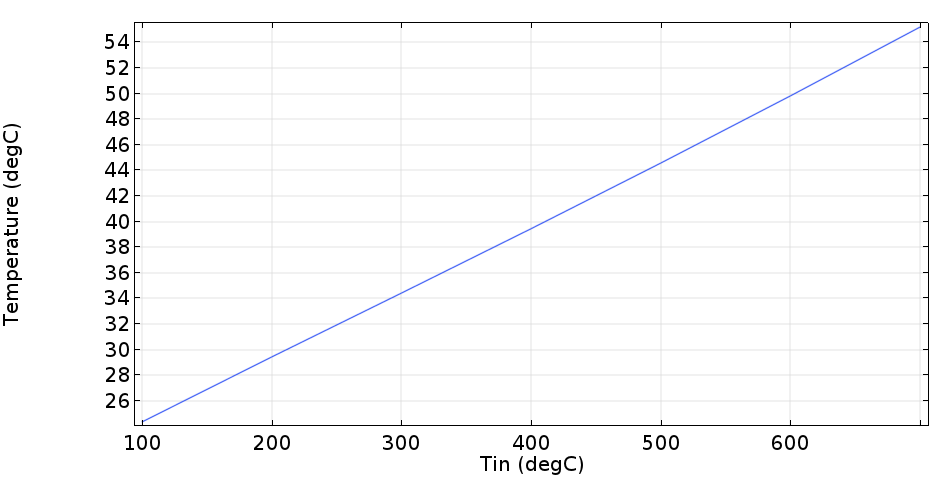
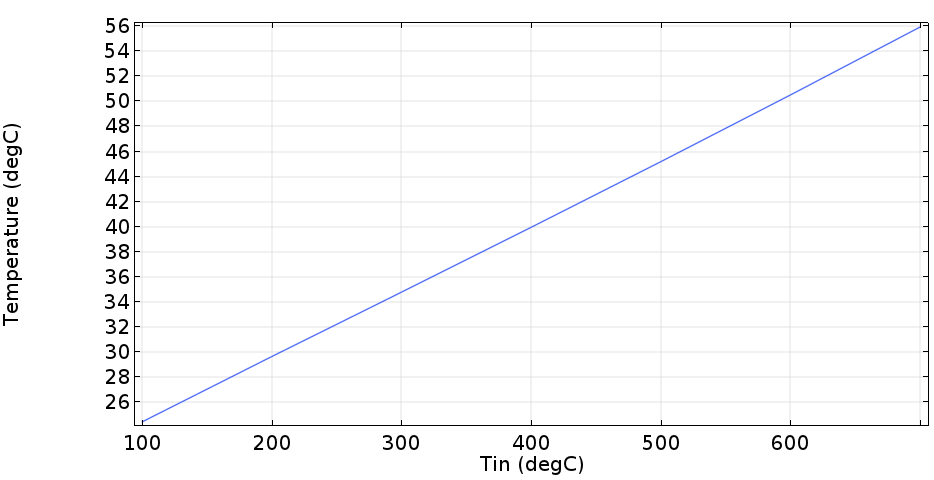
원하시는 결과인 벽면에서의 온도와 속도값에 따른 출구에서의 평균온도 값에 대한 결과를 그래프로 나타내면 하기와 같습니다.
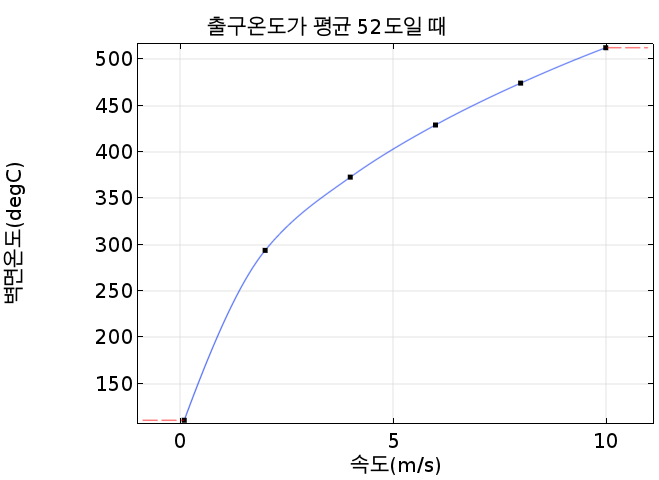
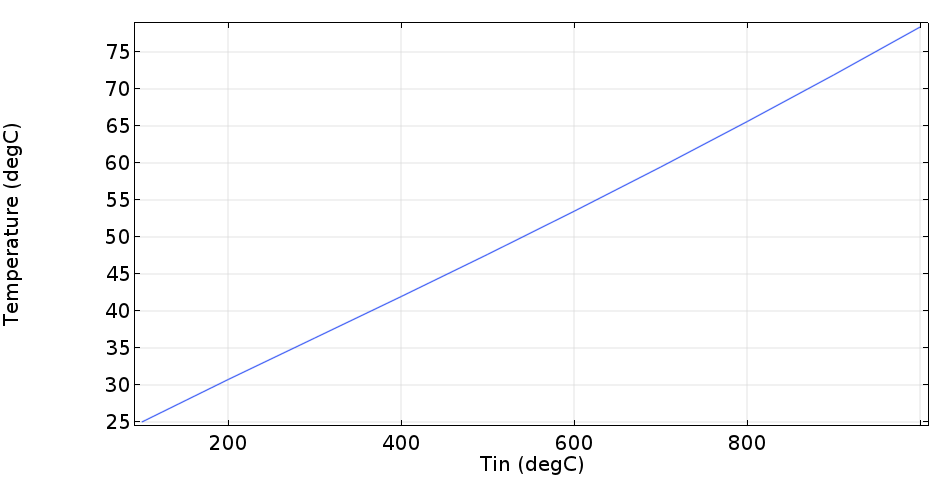
이러한 결과를 약간 가공하여 출구에서의 평균온도가 52도일때의 그래프를 보면 다음과 같습니다.
4. 결과 검토
사실 이 경우에는 어느 정도 예측 가능한 해석입니다.
이런 경우 일반적으로 열유동 쪽에서는 열적 발달유동이라고 해서, 일정한 폭 D를 가진 파이프 내에 유동이 흐를 경우, 벽면에서의 온도에 따라 열전달이 되는 경우에서는 벽면에서부터 열이 중앙부로 나아가게 되는데, 속도가 빠를 수록, 이 온도가 평균적으로 퍼지는데 더 긴 채널을 지나야 합니다.
현재의 경우 온도 가열부가 벽면 전체가 아닌 중앙의 일부라는 차이점이 있으나, 실제로 가열되는 부분이 철이기 때문에 정상해석시 전도에 의한 열전달로 채널 끝까지 열이 원할하게 전달됩니다.
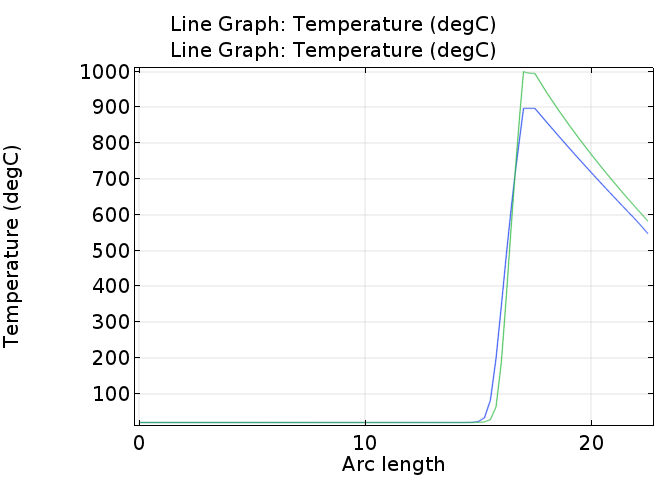
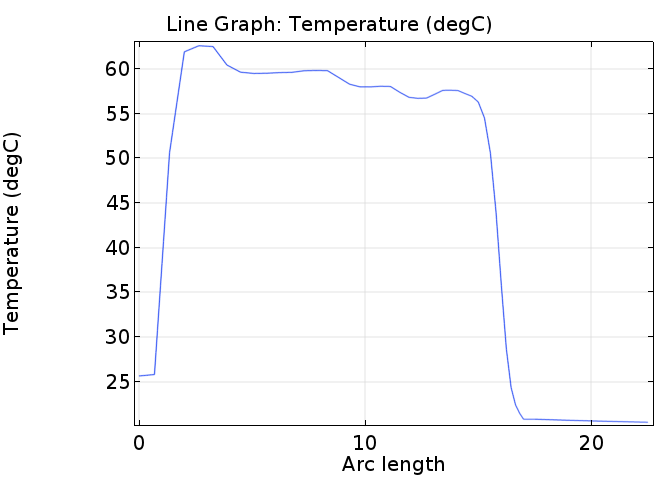
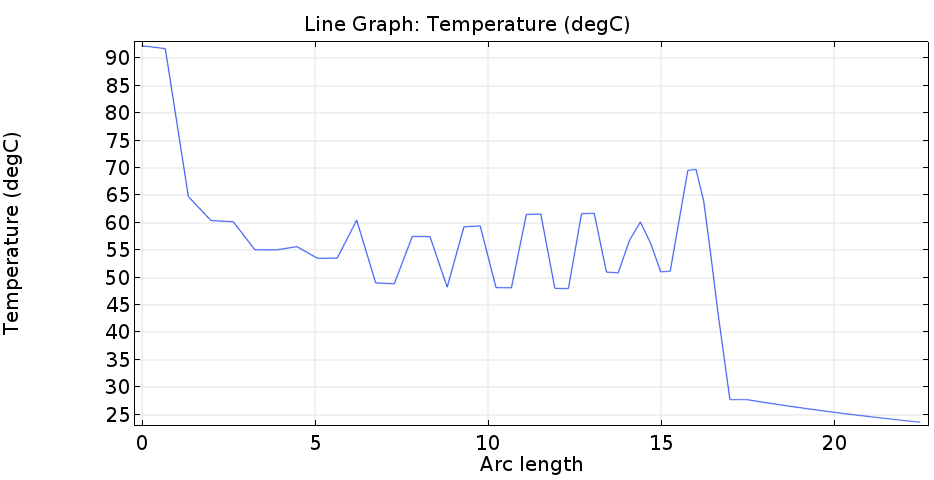
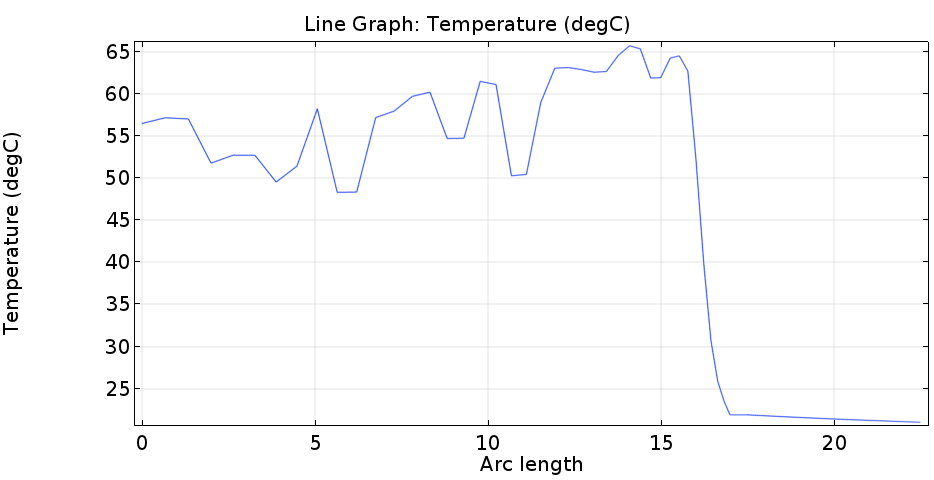
하기에 유동 채널 뿐만 아니라 철 및 단열재까지 하여 10m/s, 1000도일 때의 온도 분포를 보면 하기와 같습니다.
여기서 파란 선이 1번(출구 부분) / 녹색 선이 2번(열원이 존재하는 끝부분),에 대한 온도를 나타냅니다. 그림에서 처럼 철 재질의 경우 전도도가 굉장히 높기 때문에 출구쪽이라도 약 900도 정도의 온도를 유지하게 되는데, 이로 인하여 철제 부분의 온도가 주변 유동의 온도에 비해 굉장히 높으므로, 열원이 계속 유체에 인가되게 됩니다.
다만 이런 것으로 인해 실제로 헤어드라이기에 이런식의 가열은 굉장히 큰 단점을 수반하게 됩니다.
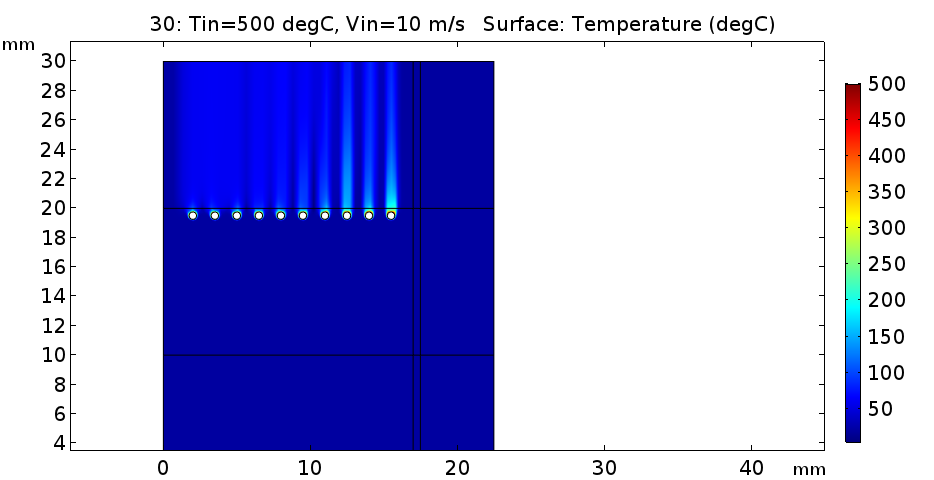
앞서 결과에서 10m/s일 경우 평균온도를 유지하기 위해서는 대략 500도 정도의 온도가 필요하다는 것을 확인 하였기 때문에, 10m/s, 500도에서의 출구쪽 결과를 추려보면 다음과 같습니다.
이렇게 되면 유체의 속도로 인해 열적 발달이 충분히 일어나지 않았습니다.
비록 이 경우에 출구의 평균 온도가 52도로 유지되지만, 실제로는 재부분의 부위에서 유체의 온도는 52도이고 벽면에서의 온도가 450도를 근접하기 떄문에 평균자체가 올라갔을 뿐입니다. (결과에서 17mm까지는 출구이며, 5mm의 철, 남은부위는 단열재입니다.)
드라이기에서 이럴 경우 큰 문제가 생기게 되겠죠.
5. 기타 해석
이를 처리하기 위해 간단한 몇 가지 케이스에 대한 해석을 수행해 보았습니다.
5.1 center부분에 두께 5mm의 내부가 빈 원통으로 열원을 구성하고 진행한 해석
이 경우 중앙에 사각형 형태의 열원을 넣었으며 유체의 원할한 진행을 위하여 위아래 부분은 라운딩 처리를 하였습니다.
아래에 위치한그래프에서 보듯이 이 경우 약 900도에 가까운 온도가 되어야 출구에서의 평균온도가 52도가 됩니다.
이 경우 열원과 철 도메인이 서로 붙어있는 상태가 아니기 때문에 열원으로 부터 유동으로 전달되는 에너지가 적고, 이에 따라 평균온도를 높이기 위해서는 많은 열에너지가 필요합니다.
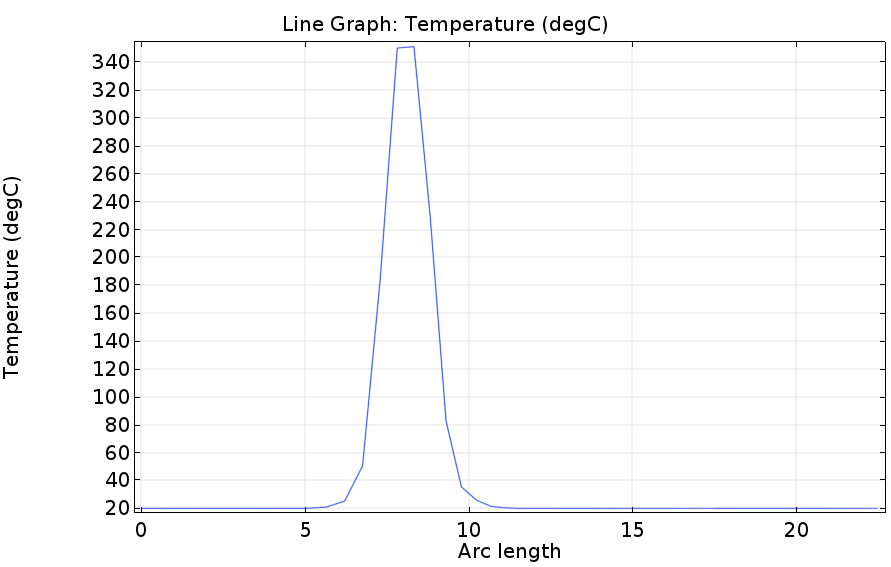
다만 하기의 그래프와 같이 출구쪽에서의 최고온도는 340도 정도로 앞서 보았던 원통 끝에서 전달되는 것에 비하여 최고온도가 낮은 편입니다.
5.2 center부분에 두께 반지름 2.5mm짜리 원을 10개 세로로 구현해 놓은 형태
앞서 형상이 중앙부에 원통이었다면 이번에는 지름 5mm(앞선 사각형과 같은 두께)원형 코일을 10개 세로로 구축해 보았습니다.
이럴경우 유체와 열원이 접촉하는 면적이 늘어나기 때문에(같은 온도를 맞추기 위해서는 열원에서 더 많은 에너지를 넣어주어야 하지만) 더 적은 온도에서 평균 52도를 맞추어 줄 수 있습니다. 이유에 대해 말씀드리면 면에서 열전달의 경우 W/m^2로 같은 물질경계라고 하였을 때, 단위 면적이 늘어날수록 열 에너지가 더 많이 전파되기 때문입니다.
하기 그래프에서 보듯이 이 경우에는 약 700도 정도에서 52도를 만들어 주네요
역시 면적이 늘어나는 만큼 열전달이 많이 일어남으로 낮은 온도에서의 평균온도를 맞춰주는 것이 가능합니다.
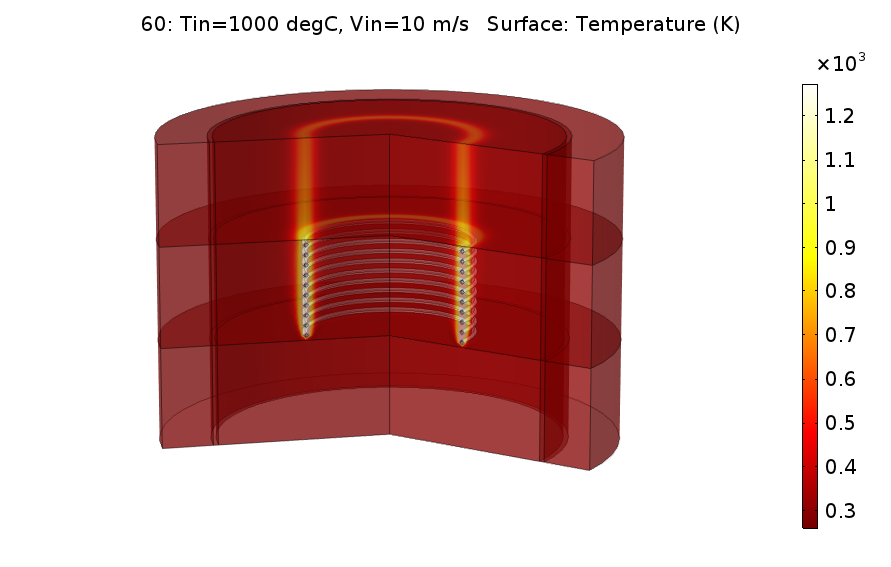
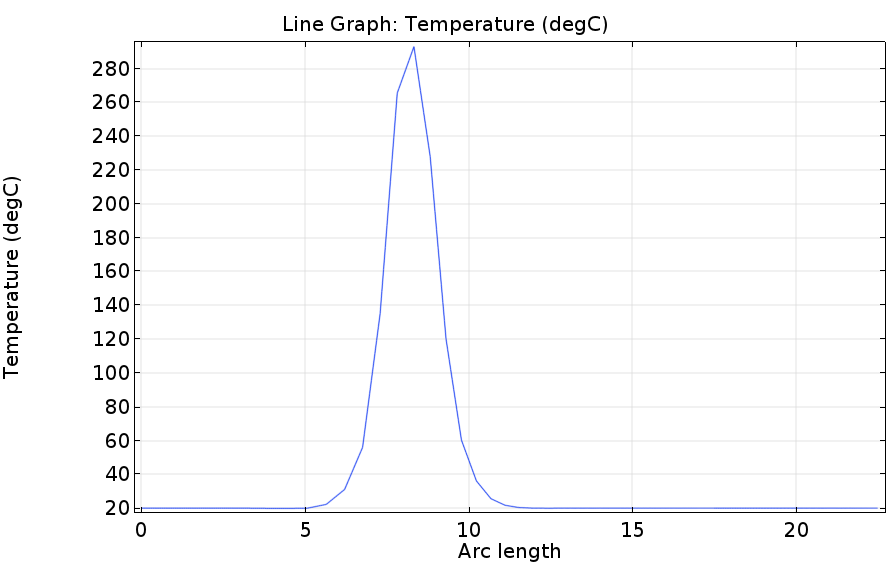
온도가 내려가긴 했지만 역시 중앙부 온도가 280~90정도로 높습니다. 하지만 앞선 결과에 비해서는 코일 중간 부분에서 유동흐름이 생기기 때문에 열이 더 넓은 면으로 분포가 되는 것이 확인가능합니다.
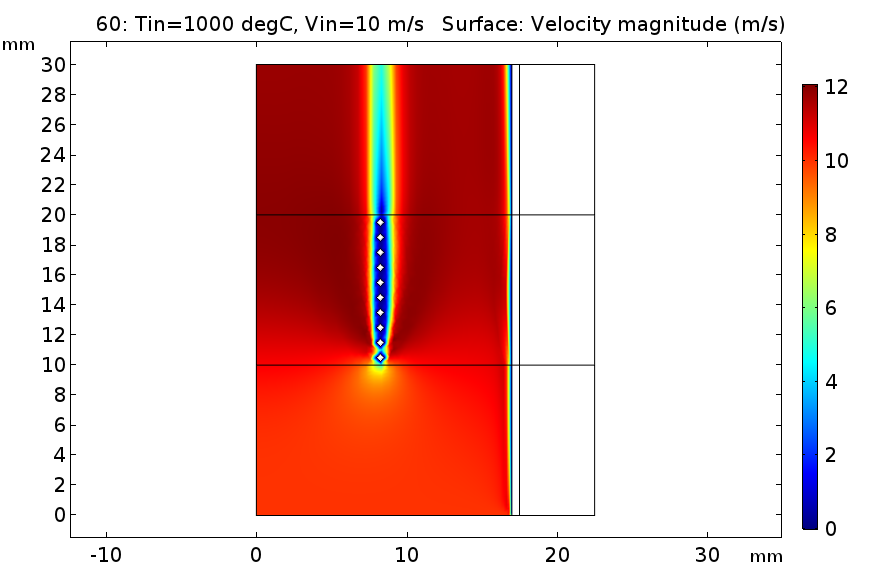
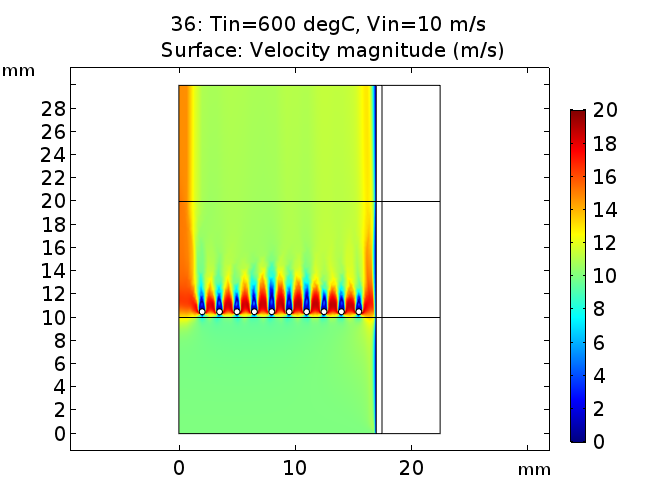
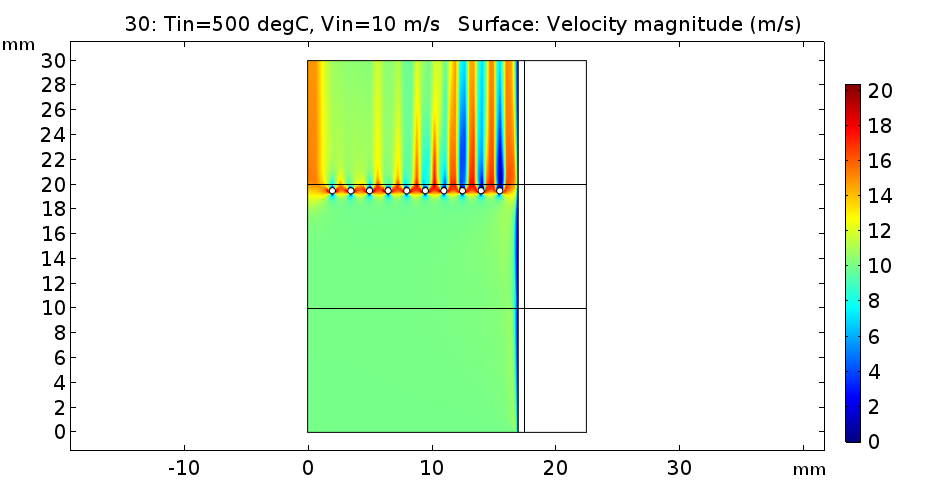
유속은 대충 이런느낌 입니다.
5.3 이번에는 보다 열을 많이 분산시키기 위하여 가로 방향으로 원을 배치해 보았습니다.
열원이 위치한 하단부에 역시 반지름 2.5mm의 원을 가로 방향으로 10개 배치한 상황입니다.
이 경우 필요한 온도는 더 떨어져셔(결국 출구 평균 온도와 관련되었기 때문에 옆으로 온도를 주는것이 최고 온도는 낮더라도 평균온도를 맞춰 주는 것이 좋죠 약 600도 내외로 평균온도 52도를 맞춰 줄 수 있습니다.
유속의 경우 조금 아쉽긴 한데 초기 열원을 조금 더 중심부에 가깝게 만들고 열원 사이간격을 조정하면 더 아름답겠네요.
참고로 여긴 넣지 않았지만, outlet에서의 평균 속도는 600도 기준 11.1m/s정도가 나옵니다. 초기 속도에서 열에의한 대류효과로 속도는 증가합니다.
5.4 필요한 온도를 떨어뜨리기 위해 이번에는 열원을 출구 방향으로 배치시켜보았습니다.
열원이 위치한 하단부에 역시 반지름 2.5mm의 원을 가로 방향으로 10개 배치한 상황입니다.
출구와 가까운 만큼, 온도도 적은 온도가 필요하며 약 450m/s에서 평균온도 52도를 유지합니다.
500도 기준 온도 그래프입니다.
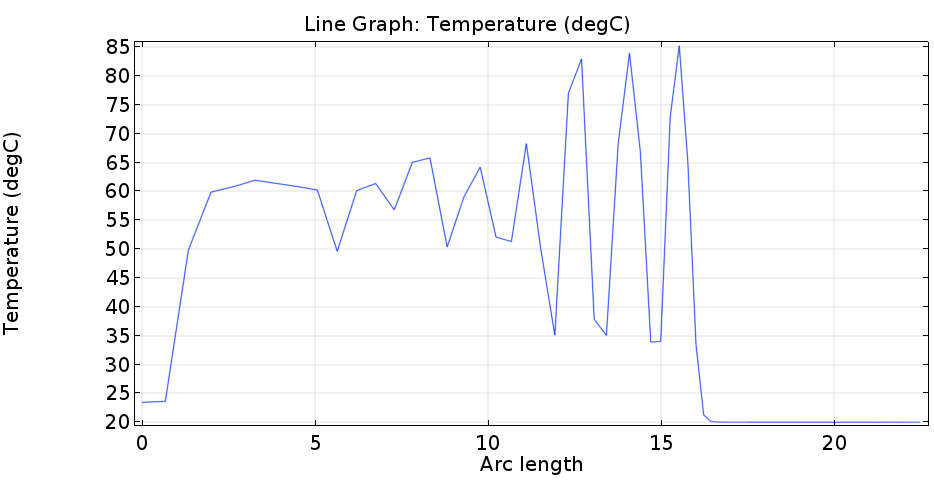
어라? 결과를 보면 아까에 비해서 외부쪽의 온도가 들쑥 날쑥함을 보여줍니다. 이 부분을 자세히 보기 위하여 단면 온도를 측정해 봅니다.
이러한 이유는 이 해석 자체가 축대칭이기 때문에 바깥쪽으로 갈 수록 표면적이 넓어지기 때문입니다. (위의 회전된 그림 참조) 따라서, 코일의 단면적이 앞에 비해 뒤로 갈수록 대류현상이 적게 일어나고 이 사이공간을 지나가는 유체의 양이 늘어남으로 인하여 온도 분포가 불균일하게 일어납니다.
바로 이전의 6.3의 경우 온도에 의한 대류효과가 채널을 지나가면서 충분히 양 옆으로 퍼졌다면, 이번의 경우 유체가 지나갈 길이가 짧기 때문에 이러한 효과를 충분히 받지 못했다고 생각됩니다.
5.5 마지막 테스트
긴 글 읽으신다고 고생이 많으셨습니다. 이제 대망의 마지막 테스트입니다.
사실 온도 분포를 균일하게 하는 가장 좋은 방법은 열원 자체를 원판형으로 두어 앞부분에 두는 것이지만, 이 경우 코일이 유체(공기)의 진행을 막게되며, 그로 인하여 유체의 흐름이 불균일하게 됩니다.
특히 이러한 원판이 클 경우, 열원을 지나는 유동흐름은 매우 불균일해지고, 실제로 중앙부에서는 유동이 지나가지 못하며, 외곽의 경우 유체가 가속될 것이므로, 열원 이후 채널의 폭이 충분히 길지 않다면 온도의 불균형이 더욱 심화될 가능성도 있습니다
이에 따라 형상수정을 조금 하였습니다. 현재 옆으로 배치한 원의 경우 중앙부분에서 온도가 너무 떨어지는 것으로 확인이 되어 최초 코일을 드라이기 중심부 쪽으로 옮겼습니다.
온도 관점에서는 열원이 가까이 있을수록 적은 온도로 출구쪽 온도를 맞추어 줄 수 있기 때문에 6.4와 같은 높이에서 원을 배치하였습니다.
다만 6.4 테스트에서 외곽으로 갈 수록 온도 구배가 큰 것을 확인하였으며, 이는 열적 발달이 충분히 일어나지 못했기 때문이라 생각합니다. 따라서 외곽의 경우에는 열원이 너무 출구쪽으로 붙으면 안된다고 생각하여, 다소 온도를 높이더라도 평균적인 온도를 맞추기 위해 열원을 외곽으로 빠질수록 아랫쪽에 배치하였습니다.
물론 이러한 테스트의 경우 이론을 바탕으로 계산을 수행하거나 다양한 케이스 스터디를 통해 보다 정확한 값을 얻어내는 편이 효율적이지만, 저의 경우에는 일단 임의로 주었습니다. (대략적인 양상을 구하기 위함이니까요)
또한 이미 6.3과 6.4에서 평균 온도 52도를 만드는데에는 코일의 온도가 500-600도 이하의 경우에서 만들어 진다는 것을 알았기 때문에, 온도에 대한 케이스는 100~700도까지만 주었습니다.
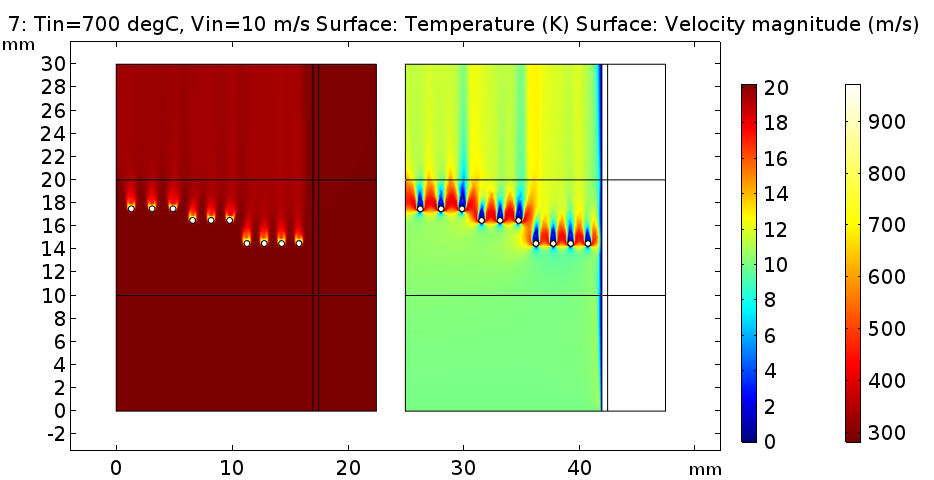
그 결과입니다. 다른 결과의 경우 모두 1000도, 10m/s에 대한 결과를 첨부하였지만, 이 경우 700도, 10m/s 결과를 첨부합니다.
어짜피 내부 형상등을 보기위해 넣었던 것이고, 이 경우 1000도까지 테스트는 수행하지 않았으니까요
결과를 보면 좌측으로 치우쳤기 때문인지 약 650도 정도에서 52도를 보여줍니다. 실제 넓은 공간을 차지하는 부분에 대해 열량이 덜 들어갔으니, 그런 것이라 생각합니다.
위와 마찬가지로 출구쪽에서의 온도 결과는 하기와 같습니다.
700도에서의 결과로 평균 온도 54도일 때의 결과입니다.
대략적으로 준 형상인 관계로 결과가 여전히 아쉽습니다.
특히 이 형상의 경우 좌측으로 붙인다는 것이 너무 붙였는지 다른 결과와 다르게 중앙에서의 온도가 너무 높습니다.
특히 외곽으로 갈수록 심해지는 온도의 불균형은 여전히 높은 위치에 열선이 있다는 것을 의미하는 듯합니다.
실제 원하는 해석을 위해서는 최초 열원을 조금더 우측으로 옮기고, 우측 열선들은 값을 내린 후에 사이간격을 조금 좁혀야 할듯 합니다.
물론 드라이기를 빠져나가는 순간 대류가 더 일어나겠지만, 최대값과 최소값의 차이가 40도 가량이 나면 드라이기로의 효용성이 의심됩니다.
또한 너무 좌측으로 붙여서 열원을 생성시켰기 때문에, 평균온도를 올리는데 너무 많은 온도를 필요로 합니다.
그래서 다시 바꿨습니다.
대략 630도 전후에서 평균온도 52도를 유지합니다.
700도일 때, 평균온도는 55도 이며 이 결과는 하기와 같습니다.
이번에는 최고 온도와 최저 온도가 15도 정도 차이가 납니다.
이 정도면 드라이기로 사용할 수 있을 것 같습니다.
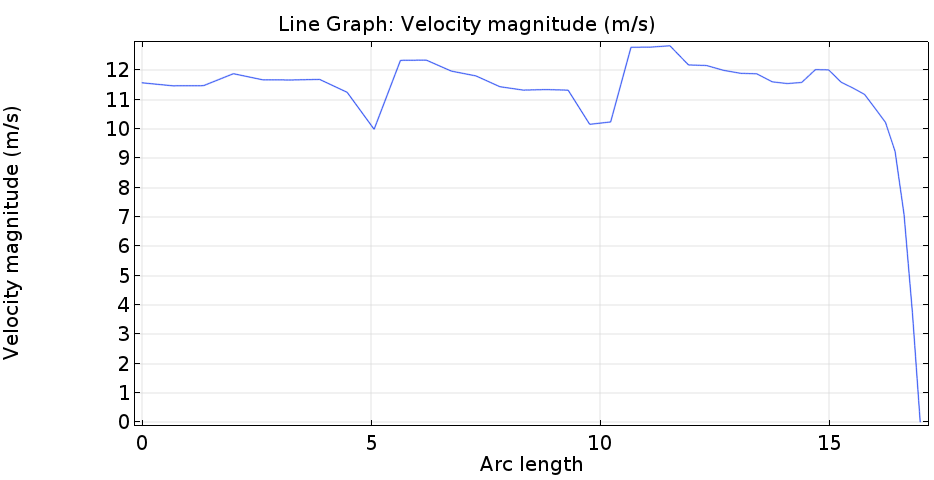
하기는 드라이기에서 나오는 유속입니다. (유속채널의 경우 17mm까지 임으로 아크렝스는 17mm까지의 결과만 나옵니다.
평균 유속은 11.2m/s 입니다.
가열에 의한 유속 변화가 있지만 채널 폭이 충분히 길기 때문에 어느정도 평균속도로 나와주네요
단면 컷에의한 온도 및 유속입니다.
6. 후기
사실 테스트 하려고 하던 해석이 아니었기 때문에 짬을 크게 내지 못해서 시간이 많이 걸렸습니다.
아쉬운점은 대략적인 경향성 테스트를 하려 했던 것이기 때문에, mesh를 조밀하게 짜지 못하여 결과가 튀는 부분이 많이 보입니다.
또한, 최종 결과를 조금 더 평균적인 값으로 가져가려 했으나, 실제 제작하려고 하는 형상도 아니고 말 그대로 임의로 코일 사이즈 등을 맞춰서 해석하였기 때문에, 결과가 어설프게 나온것이 마음에 들지 않습니다.
또한 간단한 2차원 축대칭이기 때문에 무시된 점이 너무 많습니다.
실제의 경우 코일이 저런식이 아니라 얇은 코일이 돌돌 말려있는 형태의 열원을 취급함으로 표면적이 제가 했던 것보다 훨씬 넓어질 것입니다. 그러면 당연히 코일의 온도가 해석보다 낮아지더라도 평균온도가 맞춰질 것입니다.
그리고 해석에서 radiation을 무시하였는데, 실제로 온도차가 수백도가 생기게 될 경우(코일과 주변부) 이 효과를 간단하게 무시할 수 있을 만큼 작은 온도는 아닙니다.
이 두개만 보더라도 실제와 해석에서는 차이가 많습니다. 또한 내부의 디테일한 형상들을 챙기게 되면, 고려해야할 사항은 더욱 많아지겠지요.
다만 코일 배치 등에 대한 참고정도는 될 것 같습니다.
이상 후기를 마치겠습니다. 긴 글 읽어주셔서 감사합니다.