미분방정식(2)
2012년 11월 7일 수요일
오전 3:47
두번째 시간이네요~~^^
오늘 책 진도를 나가야 하는데… 저번시간에 하다 만 얘기가 남았죠?
왜 이렇게 선형이냐 아니냐에 목숨을 거는지…
이건 제가 3학년때 양자역학에 너무 재미를 붙여서
4학년때는 대학원 수업을 청강하기까지 했는데요
그때 사쿠라이 modern quantum mechanics를 읽다가 깨달은 사실이 있었어요
미분방정식이든 뭐든 물리에서 행하는 모든 연산은
우리가 관찰하려는 "대상"이 가지고 있는 모든 정보중에서
우리가 알고싶어하는 "물리량"을 꺼내보려는 행위이다.
이건데요. 양자역학을 배우다보면 브라켓 표기법이 나와요
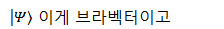

즉, 양자 상태를 하나의 벡터처럼 생각하고 문제를 풀어나가는 것 입니다.
그런데 벡터랑 벡터를 "내적" 하면 관찰하려는 물리량을 꺼내어 볼 수 있죠?
그래서 연산자중에 관찰대상의 물리적 상태는 변화시키지 않으면서
관찰하려는 물리량을 꺼낼 수 있는 연산자를 projection operator 라고 해요

암튼 저 projection이라는 단어를 보는 순간
뭔가 머릿속이 환해지는 기분이 들었어요
내가 여지껏 왜 하는지도 모르고 해 왔던 계산들은

미분방정식을 풀면 차원이 증가하거나 감소하거나 하죠?
차원이 증가하면 | 관찰한 결과를 종합해서 그 물체의 원래 상태를 추리하는것 |
차원이 감소하면 | 물체의 여러가지 정보중에 원하는 정보를 꺼내는 것. |
이렇게 생각하시면 되요~~
예를 들면, 음… 운동방정식으로 예를 들어볼게요
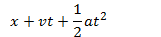
이걸 그래프로 그려보면
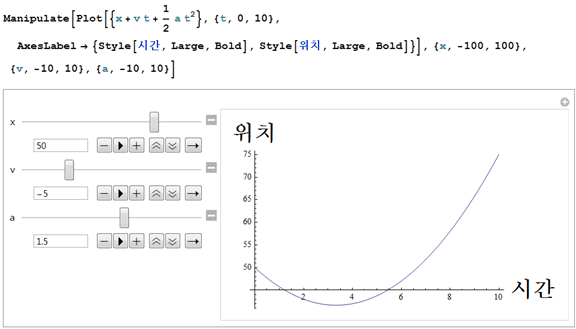
이렇게 2차함수 그래프가 그려지죠?
이 때, 초기값으로 출발위치, 초기속도, 가속도를 설정 해 주면 몇 초 뒤에 어디에 위치할지 알 수 있습니다.
다른말로 표현하면... 시간에 따른 위치를 전부 다 점을 찍어놓으면 위의 그래프가 그려지는 것이죠?
그런데 저걸 한 번 미분하면?
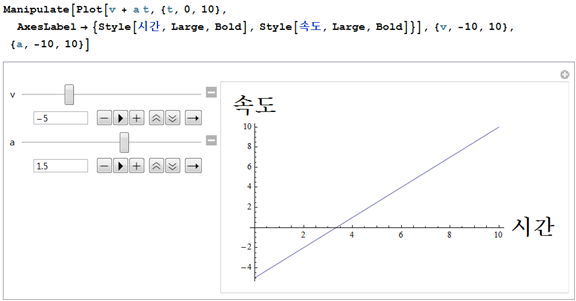
이렇게 1차함수 그래프를 볼 수 있고, 시간에 따른 "속도"를 알 수 있죠?
그래프 그릴 때 미분연산자를 써서 하려다가
어디선가 미분불가능한 지점이 생겨서 그래프가 오류가 나더라고요 ㅋ
그래서 그냥 미분한 식으로 그래프 그렸습니다 ^^;
암튼 중요한건, "위치"를 미분했더니 "속도"를 알 수 있었다.
다른말로 하면
"미분"이라는 연산자는 "위치"라는 상태로부터 "속도"라는 물리량을 뽑아내는 역할을 한다.
라고 생각하면 됩니다.
그런데 이게 왜 벡터랑 상관이 있고 프로젝션이랑 뭔 상관이냐고요? ㅋ
자... 차원이 낮아진다는 것은 무엇을 뜻할까요?
이렇게 생각해 보세요~
우리는 3차원 공간에 살고있는 3차원 물체입니다.
그런데 태양빛을 받으면 땅바닥에 그림자가 생기는데 그림자는 2차원이죠?
물리에서 Projection을 한다는것은
물체의 상태에 연산자(태양빛)을 적용해서 관측하고자하는 물리량(그림자)를 도출하는 것입니다.
이걸 벡터에서는 "내적"이라고 하죠?
내적은 영어로 inner product
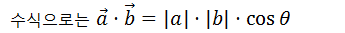
그림으로 표현하면
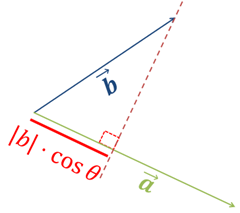
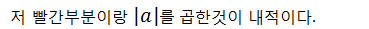
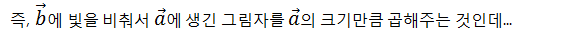
그래서 이런걸 projection이라고 한다.
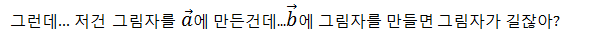
근데... 내적이 똑같다고?
네...ㅋㅋ 똑같아요 ^^
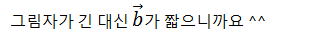
자... 그럼 벡터 내적이 그림자를 만드는것이라는 아이디어를 고대로 가져오면
3차원 물체의 그림자는? 2차원이 되고,
2차원의 그림자는? 1차원이 되고...
앗!!! 그렇군!!!
위치라는 정보를 미분한다는 것은 속도라는 벡터공간에 위치정보의 그림자를 만들어 주는 것이구나!!!
이런겁니다 ^^
선형대수학 보면 "단위벡터"라고 나오죠?
이 단위벡터는 그림자 값이 바로 물리량이 되도록 그 크기를 1로 정해둔 것들인데... 이 단위벡터들의 역할이 하나 더 있죠?
바로 좌표축을 설정하는 놈들입니다.
이런 아이디어를 다 합치면...
a. 관측 결과들을 종합하면 물체의 정보가 고스란히 담겨있는 상태를 추리 할 수 있다. (가속도, 속도를 알면 몇 초 뒤의 위치를 알 수 있는 것)
b. 모든 정보가 담겨있는 상태에 연산자를 적용하여 그림자를 만들면 원하는 물리량을 뽑아 낼 수 있다. (위치랑 시간으로 속도랑 가속도를 계산 할 수 있는 것)
이해가 안되실까봐 그림으로 보여드리면...

송중기의 정보를 알면 생일, 키, 몸무게는 바로 알 수 있죠?
그리고... 만약에 누가 사람을 죽여서 경찰들이 막 수사를 해요
그랬더니 범인의 키는 178이고 몸무게는 65이고 생년월일이 1985년9월19일이다.
이걸 알아내면
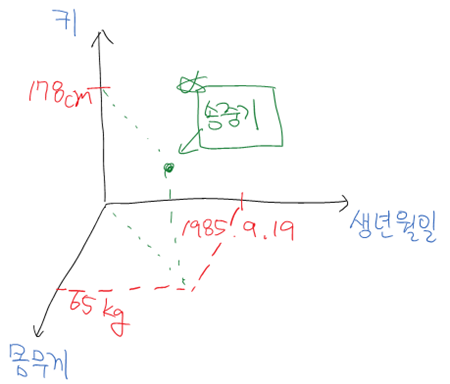
이렇게 좌표축에서 역추적해서 범인이 송중기라는 것을 알 수 있는거죠
송중기 이 나쁜새끼
사람을 죽이다니... ㅡ.ㅡ
(절대 나랑 나이도 같은게 잘생기고 멋있어서 질투나서 이러는거 맞음 ㅡ.ㅡ)
암튼... 그래서 저번시간부터 선형이니 아니니 자꾸 파고든겁니다.
결국은 선형공간에서는 연산자의 역할이 다 물리량 뽑아내는 것이거든요
아니면 물리량 주고 최종상태 추리해라 이런거...
그리고 비선형이면... 그림자가 안생겨요 ㅜ.ㅜ
저기 저 좌표축을 이루는 독립변수들이 종속변수랑 꼬여있으면
그림자를 그리면 그 그림자가 원래상태에 또 영향을 줘서 계속 꼬이고 꼬이고....
그래서 비선형이 어려운겁니다 ㅡ.ㅡ
암튼 오늘의 결론은
1. 선형미분방정식은 그림자를 만드는 연산자이다.
2. 그림자는 우리가 관측가능한 물리량이다.
3. 그림자를 조합해서 원래 상태를 추리할수있다.
4. 원래 상태를 알면 이쪽 저쪽에서 빛을 비춰 원하는 그림자를 뽑아 낼 수 있다.
이겁니다.
그럼... 다음시간부터 다시 책 진도 나갈게요~~
빠이염~~~~
아!! 그리고 매스매티카 파일도 첨부할게요
매스매티카 7로 제작하였습니다.
 운동방정식.nb
운동방정식.nb
Microsoft OneNote 2010을(를) 사용하여 작성했습니다.
모든 노트 및 정보를 한 곳에서 볼 수 있습니다.





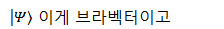



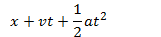


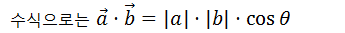

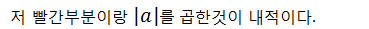
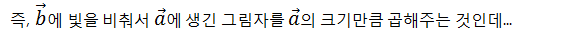


 운동방정식.nb
운동방정식.nb









