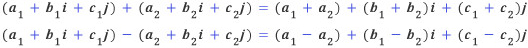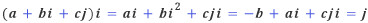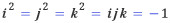대수적 관점에서 수의 확장을 생각할 때, 복소수는 더 이상 확장할 수 없는 가장 큰 수체계라 할 수 있다. 그렇다면 다른 관점에서 복소수를 확장할 수는 없을까?

기하적 확장

계수가 복소수인 다항식의 근은 항상 복소수가 된다고 하였다. 이 사실은 대수학의 기본 정리라 불리는 것으로, 이런 관점에서는 복소수보다 더 큰 범위의 수는 없다고 할 수도 있다. 그러나 다항식의 근이라는 관점이 아닌 다른 관점에서라면 당연히 복소수보다 더 큰 범위의 수를 생각할 수 있다. 예를 들어, 복소수의 제곱근이 복소수 i가 될 수는 없으므로, 제곱근이 i가 되는 새로운 수를 이용하여 복소수를 확장할 수 있다. 그렇지만 사실 이런 새로운 종류의 수는 그다지 쓸모가 없다.

실수에서 복소수로 수의 범위를 확장하는 것은 다항식의 근을 구하는 관점에서 확장하는 것이기도 하지만, 한편으로는 수직선을 평면으로 확장한 것이기도 하여 그 기하적 성질로부터 좋은 결과를 수없이 이끌어낼 수 있다. 그렇다면 복소수를 기하적 관점에서 확장하는 방법은 무엇일까? 독자들 대부분이 눈치챘겠지만, 복소수가 나타내는 평면을 확장하여 공간을 묘사하는 수를 만들어내는 것이 바로 그 방법이다.

공간을 나타내는 수

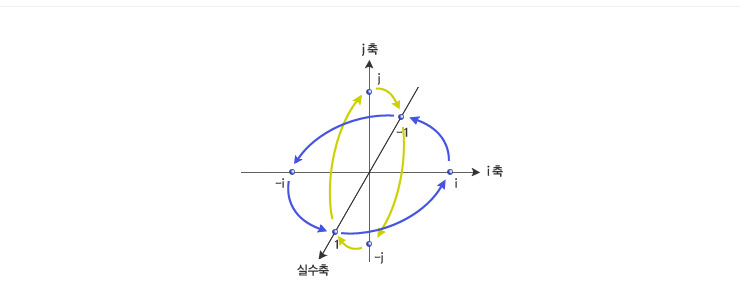
평면은 2차원이므로 평면을 나타내기 위해서는 실수축과 허수축의 두 축이 필요하다. 마찬가지로 공간은 3차원이므로 공간을 나타내기 위해서는 세 개의 축이 필요하다. 따라서 복소평면에 새로운 허수축을 하나 덧붙이면 될 것 같다. 새로운 허수단위를 j로 나타내면, 복소수를 확장한 새로운 수는, a, b, c를 실수라 할 때 a+bi+cj로 나타낼 수 있다. 이 수를 세 개의 요소가 필요하다는 뜻에서 삼원수(三元數)라 부르기로 하자. 이 수는 명백히 공간의 한 점을 나타낼 수 있고, 덧셈과 뺄셈도 자유롭다.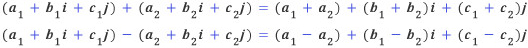

여기까지는 어느 수학자라도 생각할 수 있는 착상이고 독자들 가운데도 똑 같은 생각을 한 사람이 있을 것이다. 그런데 문제는 곱셈이다. 아무렇게나 곱셈을 정의할 수도 있겠지만, 기왕이면 복소수의 곱셈을 확장하는 편이 좋을 것이다. 다시 복소수의 곱셈을 생각해 보면, 그 기하적 의미는 원점을 중심으로 한 회전변환이라 할 수 있으므로, 삼원수의 곱셈 또한 원점을 중심으로 한 회전변환이 되는 것이 가장 자연스럽다.

이제 몇 가지 삼원수에 대해 실험을 해 보자. 실수 1에 허수단위 i를 곱하는 것은 j축을 중심으로 90도 회전이동하는 것으로 생각할 수 있다. 또, 실수 1에 새로운 허수단위 j를 곱하는 것은 i축을 중심으로 90도 회전이동하는 것으로 생각할 수 있다.

이런 식으로 회전이동을 묘사하면 삼원수라는 것도 꽤 그럴 듯하다. 이제 실수축을  중심으로 90도 회전이동하는 방법을 생각해 보자. 이것은 i에 곱하여 j가 나오는 수를 찾으면 된다. 좀전과는 달리 얼른 떠오르지가 않으니, 그 수를 a+bi+cj라 하고 i에 곱해 보자.i2 = j2 = -1이므로, 다음을 만족하는 실수 a, b, c를 찾아야 한다.

양변을 비교하면, a=b=0이 되는데, j와 i의 곱 ji가 j나 -j일 수는 없으므로 결국 위 등식을 만족하는 실수 a, b, c는 존재할 수가 없다. 이럴 수가!

이 난제를 맞닥뜨린 사람은 19세기 아일랜드 수학자인 해밀턴(William Rowan Hamilton, 1805-1865)이었다. 두 개의 허수단위 i와 j를 추가하여 삼원수를 만들려던 해밀턴은 곱셈과 나눗셈에서 완전히 막혀 버렸다. 몇 달을 고민하였으나 문제가 해결될 기미가 전혀 보이지 않았다.

윌리엄 해밀턴의 기념우표. 수학, 물리학에 큰 업적을 남겼다.

언어의 신동이 수학의 신동으로

아일랜드가 낳은 최고의 수학자인 해밀턴은 어렸을 때 수학 신동보다는 언어의 신동으로 유명하였다. 12살 무렵에 이미 자기 나이보다 많은 개수의 언어에 능통할 정도였으니 상상을 초월하는 천재라 하겠다. 이런 언어의 천재가 수학의 천재로 바뀌게 된 계기는 해밀턴이 12살 무렵에 암산 신동 콜번(Zerah Colburn, 1804-1839)을 만난 것이었다. 자신보다 한 살 많은 소년이 암산으로 어려운 계산을 척척 해내는 것을 본 해밀턴은 큰 자극을 받고 수학 공부에 몰두하게 된다. 이후 18살에 트리니티 대학에 입학한 해밀턴은 22살에 천문학과 교수로 임명된다. 지금이야 수학, 물리학, 천문학이 분리된 학문이지만, 이때까지도 세 학문은 거의 구별되지 않을 때였다. 해밀턴의 가장 큰 학문적 업적이라 할 해밀토니안(Hamiltonian)도 물리학과 관련된 내용이었다.

트리니티 대학의 교수로 수많은 업적을 쌓아가던 해밀턴은 1843년 무렵에 복소수를 확장한 수를 연구하고 있었다. 여전히 별다른 진전이 없던 1843년 10월 16일, 해밀턴은 부인과 함께 더블린의 왕립 운하를 따라 걷고 있었다. 삼원수의 곱셈에 대해 끊임없이 생각하고 있던 해밀턴의 머릿속에 번쩍하는 아이디어가 떠올랐다. 허수축은 두 개가 아니라 세 개가 필요하며, 곱하는 순서가 바뀌면 그 결과도 달라진다는 것이었다. 해밀턴은 주머니를 뒤졌지만 이 아이디어를 적어놓을 만한 종이를 찾을 수가 없었다. 해밀턴은 근처에 있던 브로엄 교(Brougham bridge)의 난간에 칼로 다음과 같이 새겨 놓았다.

암호 같기도 한 짧은 내용이지만, 오랫동안 연구를 해온 해밀턴에게는 문제를 해결하기에 충분하였다. 집에 돌아온 해밀턴은 서둘러 새로운 수체계를 만들어내었다. 이 수는 실수 성분 하나와 허수 성분 세 개가 필요한 수여서 이제는 삼원수가 아니라 사원수(四元數, quaternion)라 불리게 되었다.

사원수

사원수는 세 개의 허수단위 i, j, k를 이용하여 a+bi+cj+dk 꼴로 나타낸다. 여기서 i, j, k는 제곱하여 -1이 되는 허수이며, 각각의 곱은 다음과 같이 정의된다.

보다시피 i와 j의 곱은 곱하는 순서에 따라 부호가 달라진다. 실수나 복소수에서는 곱하는 순서가 바뀌어도 그 결과가 같은데, 이것을 교환법칙이라 한다. 이 당연해 보이는 교환법칙이 사원수에 대해서는 성립하지 않아 수학자들을 놀라게 하였다. 이런 구조를 비가환(非可換, noncommutative)이라 하며, 사원수는 처음으로 발견된 비가환인 수체계였다. 그러나 한편으로는 사원수가 비가환이 되는 것은 당연한 일이기도 하다. 삼차원 공간에서 회전변환을 생각하면, x축을 중심으로 먼저 회전하고 그 다음으로 y축을 중심으로 회전하는 것과, 순서를 바꾸어 y축을 중심으로 회전한 다음 x축을 중심으로 회전하는 것은 분명히 다르기 때문이다. 해밀턴이 이 사실을 몰랐을 리는 없으므로, 해밀턴이 문제를 해결하는 데는 새로운 허수 k를 도입한다는 아이디어 하나면 충분하였을 것이다. 많은 수학 문제가 그렇듯, 돌파구가 열리는 순간 모든 것이 자명하게 이끌어져 나왔을 것이기에.

사원수로 묘사하는 공간

삼차원 공간을 나타내는 데는 세 개의 성분이면 충분하므로, 사원수는 한 성분이 남아돈다고 할 수 있다. 사실 삼차원 공간을 나타내는 데는 세 개의 허수축 i, j, k만이 쓰인다. 다음 회에는 회전변환을 묘사하기 위해 사원수의 사원수의 곱셈 등을 소개하도록 하겠다.