
| 곱셈에 기본 원리에 충실한 ‘선긋기 계산법’ 
초등학교에서 처음으로 곱셈을 배울 때 같은 수를 여러 번 더하는 것을 피하기 위하여 곱셈을 도입한다. 물론 이런 방법이 곱셈의 정확한 의미를 모두 포함하고 있지는 않지만 곱셈의 기본 원리는 충분히 설명하고 있다. 일명 ‘묶어서 세기’인 이 방법은 기하학적으로 설명할 수 있다. 이를테면 3×7은 3+3+3+3+3+3+3=21인데, 이것은 왼쪽 아래 그림과 같이 3개의 직선과 7개의 직선이 몇 개의 점에서 만나는 것인가를 묻는 것과 같다. | |
| |
| | 이와 같은 곱셈법을 ‘선긋기 계산법 ’이라고도 하는데, 두 수의 곱을 직접 셈하지 않고 선을 그리기만 해도 간단하게 답이 나오는 이 방법을 간단한 예인 21×14로 알아보자. ’이라고도 하는데, 두 수의 곱을 직접 셈하지 않고 선을 그리기만 해도 간단하게 답이 나오는 이 방법을 간단한 예인 21×14로 알아보자.
먼저 아래 첫 그림과 같이 21을 왼쪽 위에 2개, 오른쪽 아래에 1개의 사선을 긋는다. 즉, 10의 자릿수만큼 왼쪽 위에 사선을 긋고 1의 자릿수만큼 오른쪽 아래에 사선을 긋는다.
| |
| 이렇게 사선이 그려진 사각형에 14를 표시하기 위하여 아래 중간 그림과 같이 10의 자릿수는 그 수만큼 왼쪽 아래에 사선으로 나타내고 1의 자릿수는 그 수만큼 오른쪽 위에 사선으로 나타낸다. 이 경우는 10의 자릿수를 나타내는 사선은 1개, 1의 자릿수를 나타내는 사선은 4개를 긋는다. 이때 선과 선이 만나는 점의 개수를 세어 보자. 100의 자리에는 점이 2개 있고, 10의 자리에는 9개, 1의 자리에는 점이 4개 있으므로 21×14의 답은 200+90+4=294이다. | |
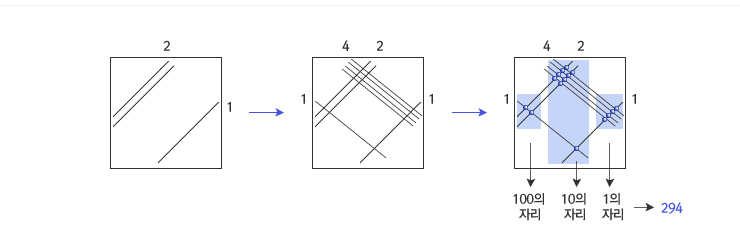
21×14를 선긋기 계산법으로 계산하는 과정

| 마찬가지 방법으로 24×23을 계산하기 위해 오른쪽 그림과 같이 사선을 긋고 선과 선이 만나는 점의 개수를 센다. 그러면 점이 100의 자리에는 모두 4개, 10의 자리에는 모두 14개, 1의 자리에는 모두 12개의 점이 생긴다. | |
| 이때 점의 개수가 10이 넘으면 위의 자리로 올려서 계산한다. 즉, 400+140+12=552이므로 24×23=552이다. 겔로시아와 마찬가지로 선긋기 계산법은 두 자릿수 곱셈만 가능한 것은 아니다. 겔로시아의 경우는 곱하는 수들의 자릿수에 맞게 격자를 그려야 한다는 불편함이 있는데, 마찬가지로 선긋기 계산법의 경우도 곱하는 수들의 각 자릿수의 개수만큼 사선을 그려야 한다는 번거로움이 있다. 따라서 큰 수를 곱할 때는 매우 불편하다. 아래 그림을 보면 그 불편함이 이해가 갈 것이다. 이런 불편을 없애기 위하여 우리가 오늘날 사용하는 가로셈법 또는 세로셈법이 등장한 것이다. | |
| | 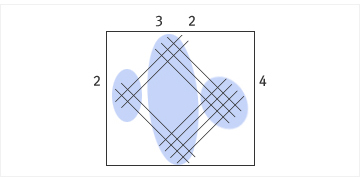
10의 자리에 점이 4개, 10의 자리에는 점이 14개, 1의 자리의 점이 모두
12개이다. 따라서, 24×23 = 400+140+12 = 552이다. | |
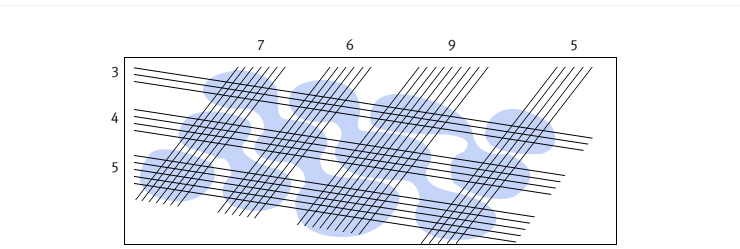
7695×543=4178385를 계산한 모습. 선긋기 계산법은 숫자가 커지면 불편해진다.

| 쉬우나 불편한 방법이 어려워도 편리한 방법으로 대체되는 것이 수학의 발전 
이처럼 수학적으로 매우 흥미롭고 간단한 방법은 적용범위가 커질수록 오히려 사용하기 불편해지기 때문에 쉽지는 않지만 편리한 방법으로 대체된다. 혹시 여러분 주위에 아직도 간단하지만 불편한 수학이 있다면 편리한 방법을 찾기 위해 도전해보기 바란다. 그런 도전이 수학을 더욱 풍요롭고 흥미로우며 즐겁게 만든다. | |
- 격자곱셈법(겔로시아 곱셈법)
수학에서 격자를 이용한 곱셈법. 이 방법을 ‘격자’라는 뜻의 ‘겔로시아(Gelosia)’라고 불렀다. 인도에서 최초로 개발된 것으로 추측된다.
- 선긋기 계산법
곱셈을 선을 그어서 계산하는 방법. 곱셈의 원리에 충실한 방법이다. 곱셈할 두 수를 자리수 별로 나누어 선을 교차하게 그은 후 묶어서 세는 방법으로 계산한다.
- 글 이광연 / 한서대학교 수학과 교수
- 성균관대학교 수학과를 졸업하고 와이오밍 대학교에서 박사후 과정을 밟았다. 저서로는 [웃기는 수학이지 뭐야], [수학자들의 전쟁], 2008년 문화체육관광부 우수과학도서로 선정된 [수학블로그] 등이 있다.
http://navercast.naver.com/contents.nhn?contents_id=2550









 글쓰기
글쓰기