수학에서 점화식(또는 재귀식)(Recurrence relation)이란 수열의 항 사이에서 성립하는 관계식을 말한다. 즉, 수열 {} 의 각 항  이 함수 f 를 이용해서

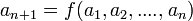
처럼 귀납적으로 정해져 있을 때, 함수 f 를 수열 {} 의 점화식이라고 하며, 또한, 수열 {} 은 점화식 f 로 정의된다고 한다.

(출처:http://ko.wikipedia.org/wiki/%EC%A0%90%ED%99%94%EC%8B%9D)

*이 정의에 사족을 좀 붙이자면 대부분의 전문서적에선 점화식을 f 혹은 F로 정의하지 않는다. 그 이유는 f, F는 대표적 점화식인 피보나치 수열을 정의할때 통상적으로 쓰이기 때문이다. 따라서 피보나치 수열을 말하는게 아니라면 대부분 h 혹은 g등을 쓰는 편이다.

점화식이란 정의가 정확히 언제부터 시작되었는지는 알수 없겠지만 점화식이란 수학적 개념은 상당히 오래된 개념이다. 또한 근래에 많은 점화식들이 정수론(number theory)이나 조합이론(combinatorics)등의 문제들에 대한 답을 제시하면서 1800~1900년대에 점화식들과 이 문제들 사이의 관계가 많이 공부되어왔다. 그러다 최근에 들어서는 많은 수학자들이 흥미를 잃고 그다지 활동이 활발하지 못한 분야이긴 하지만 최근들어 점화식을 이용한 새로운 암호작성이론(Cryptography)이 조금 눈길을 끌고 있다 (필자도 현재 이 분야에 대한 연구를 약간 하고 있는 중이다.)

보통 "점화식"이라고 하면 어려운 수학적 용어라고 생각할수도 있는데 수학/과학을 공부한 사람이라면 알게 모르게 한번쯤은 점화식의 예를 접해봤을 것이다.

F_n=F_{n-1}+F_{n-2} 

F_0=0, F_1=1.

이 점화식이 주는 수열은 {0, 1, 1, 2, 3, 5, 8, 13...} 이다. 어라? 어디서 많이 봤는데? 이 수열이 바로 그 유명한 피보나치 수열(Fibonacci sequence)이다. 피보나치 수열은 조합이론에 있는 다양한 문제에 대한 답을 주기때문에 아주 흥미로운 수열로 보여지며, 1차 점화식(First order recurrence relation)을 제외한 점화식중 가장 간단한 점화식이기에 점화식을 연구하는 사람들이 가장 먼저 보는 예시이기도 하다. 하지만 어떻게 보면 피보나치 수열보다 훨씬 더 유명한 점화식이 있다.

H_n=m*H_{n-1}

H_0=0, H_1=1, m=양의 정수.

예를들어 m을 2라고 하면, 이 점화식이 주는 수열은 {0, 1, 2, 4, 8, 16...} 이 된다. 당연히 각 수는 a_n=2^n 으로 표현될수 있다. 따라서 각 m에 따라 이 수열은 m의 곱을 표현하게된다. 즉 이 수열은 m진수의 숫자들을 모두 나열하게 되므로 이 점화식은 m진수를 만들어내는 점화식인 셈이다. 하지만 보통 1차 점화식의 경우 너무 간단하다라는 이유로 거의 언급조차 되지 않는다.

*정확한 용어로는 1차/2차 점화식이 아니라 1항간/2항간 점화식이라고 명칭되는 것으로 알고있다.

II. 특정 다항식(Characteristic polynomial).

수학 혹은 과학을 공부한 사람이라면 특정 다항식이란 단어를 한번쯤은 들어봤을 것이다. 바로 선형대수학에서 행렬(matrix)의 고유치(Eigenvalue)를 근(root)으로 갖는 식을 그 행렬의 특정 다항식, p(x), 라고 지칭한다. 헌데 점화식에도 특정 다항식이 있다. 위에서 예를 든 피보나치 수열으르 보자.

F_n=F_{n-1}+F_{n-2}

만약에 내가 백만번째 피보나치 숫자를 알고싶다면 어떻게 할까? 그냥 Python이나 Mathematica 같은 소프트웨어에 4줄짜리 코드를 집어넣으면 된다.. 가 답일수도 있다. 가장 단순무식한 4줄짜리 코드라해도 요즘 컴퓨터들은 30초안에 백만번째 피보나치 숫자를 찾을수 있다. 점화식의 결과물중 하나인 루카스 수(Lucas numbers)를 이용한다면 약 10줄의 코드로 0.1초안에 백만번째 피보나치 숫자를 찾을수도 있다.(물론 이 코드는 오차가 있기 때문에 특정숫자 이상의 피보나치 숫자를 찾을때만 쓰일수있다. 하지만 백만번째 피보나치 숫자는 충분히 크기 때문에 오차를 감안하더라도 맞는 숫자를 준다.)

자, 여기서 4줄짜리 코드에 집중해보자. 4줄짜리 코드란 단순하게 첫 두개의 피보나치 숫자(0과 1)를 집어넣고 컴퓨터에게 2번부터 100만번째까지의 모든 피보나치 숫자를 구하라고 하는 것이다. 백만개의 숫자를 30초안에 찾아낼수 있다는것은 놀라운 결과라고 볼수 있지만 피보나치 수열이 얼마나 친절한 수열인지를 감안한다면 그다지 감탄할 결과는 아니다. 보다 효과적으로 피보나치 숫자를 찾는 방법은 바로 특정다항식을 이용하는 것이다. 다음 다항식을 살펴보자.

x^2=x+1 -> p(x)=x^2-x-1.

근의 공식을 이용한다면 이 다항식의 근이 [1+/-sqrt(5)]/2 라는걸 금방 알수 있다. 자 그럼 이제 다음 식을 살펴보자

H(m)=[(1+sqrt(5)/2)^m-(1-sqrt(5)/2)^m]/sqrt(5)

이 식에 m=0, 1, 2, 3...을 대입하면 {0, 1, 1, 2, 3, 5...}의 피보나치 수열을 얻게된다. 과연 우연의 일치일까? 아니다. 만약에 점화식이 주어진다면 그 점화식을 위에 방법대로 바꿔서 특성 다항식을 얻을수 있다(이에 대한 증명은 선형대수학과 약간의 귀납법을 사용하면 쉽게 증명할수 있다. 혹은 왠만한 기본 서적에서 찾아볼수 있다). 그러면 그 특성다항식은 n차 다항식이므로 총 n개의 근을 준다. n개의 근을 a_1, a_2, ..., a_n 이라고 칭하면 점화식이 주는 수열은 다음과 같이 표시될수 있다(여기서는 두번 이상 반복되는 근은 반복되는 만큼 표시한다. 하지만 이후로 반복되는 근은 한번만 표기하도록 하겠다).

H(m)=(p_1(x)*a_1)^m+(p_2(x)*a_2)^m+...+(p_n(x)*a_n)^m

여기서 각 p_m(x)는 다음과 같은 성질을 갖는다.

1. 만약 a_m 이 특성 다항식에서 b번 반복되는 근이라면 p_m(x) 는 b차 다항식이다.

2. 다항식 p_m(x)의 계수(coefficient)는 점화식의 초기 조건(initial condition)에 의해 결정된다. 

물론 이 방법이 쉬운 방법은 아니다. 그 이유는 다항식의 근을 찾는것이 굉장히 어렵기 때문이다. 다항식의 근을 찾는 것은 선형대수학에서 행렬의 고유치를 찾는 것과 똑같은데 선형대수학의 가장큰 문제가 "행렬의 고유치를 어떻게하면 잘 찾을 수 있는가?"이며 이 문제가 지난 400여년간 조금씩 발전해왔지만 아직도 선형대수학에서 가장 어려운 문제라는걸 감안한다면 이 방법도 그다지 효율적이진 않다. 하지만 2차 점화식에 관해서만큼은 쉽게 특성 다항식의 근을 찾을 수 있으므로 적절한 방법이라고 할수 있다.

시간이 된다면 다음 내용은 2부에서 계속...