수학이 얼마나 신기한 개념들을 다루는지 소개하기 위해 이 [수학의 부스러기] 시리즈(?)를 쓰게 되었습니다. 개인적으로 생각하기에 기묘한 개념들 중, 쉽고 잘 알려진 것부터 생소하고 어려운 부분까지 차근차근 다뤄보도록 하겠습니다. 얼마나 버틸수 있을지는 모르겠지만...보완할 점 지적해주시면 감사하겠습니다(__)

=========================================



여러분은 '집합(set)'이란 개념을 잘 알고있을 것입니다. 고등학교 과정에서 집합은 아마 '어떤 구체적인 조건을 만족하는 것들을 모아놓은 것' 정도로 가르치게 될 것입니다. 집합을 구성하는 것을 '원소(element)'라고 부르고 '"원소"∈"집합"'으로 표기합니다.

예를들어 집합은 다음과 같은 것을 말합니다 : {1보다 큰 실수들의 모임}, {좌표평면 위의 점들의 모임}. 한편, {키가 170cm 이상인 10살인 어린이들의 모임} 같은 것들도 집합이 된다고 주장할 수도 있겠으나, 수학적으로 "키", "cm", "10살", "어린이" 등이 잘 정의되지 않았기 때문에(물론 잘 정의하는 방법이 있을 수 있지만 공식적으로 정의되지는 않습니다.) 수학에서는 이와 같은 집합을 다루지는 않습니다. 물론 "1", "실수", "좌표평면" 등은 잘 정의됩니다.

이제부터 어떠한 집합이 주어졌을 때 집합이 얼마나 큰지를 재는 방법을 논해 볼 것입니다. 항상 수학자들은 어떠한 집합이 주어지면 그 안의 원소들 간에 연산(operation)이나 동치관계 혹은 순서관계(equivalence relation or ordering relation) 등을 어떻게 그럴싸하게 줄 수 있는지를 생각하고자 했습니다. 방금 말한 집합이 얼마나 큰지를 따져보는 것은 순서관계에 관련되어 있습니다. '순서'란, 말 그대로 두 원소 사이에 크기비교를 주는 것으로서, 예를들어 실수 과 사이 라는 부등호를 생각하면 쉬울 것입니다.

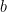
그렇다면 집합 두 집합 , 가 주어졌을 경우에 순서를 어떻게 줄 수 있을까요? 우선적으로 머리 속에 스치는 것은, 만약 , 와 같이 , 사이에 포함관계가 있으면(이 경우 를 이루는 모든 원소(즉, 와 가 모두 안에 있습니다. 이 때 를 에 포함된다고 부르고 라 표기합니다.) 와 같이 순서관계를 생각 할 수 있을 것입니다. 하지만 , 와 같이 서로 포함관계가 없다면 어떨까요? 이런 고민으로부터 곧바로 떠오르는 생각은
'에는 원소가 2개고 에는 원소가 3개이니까 가 더 크다고 하면 되겠다!'
정도 일 것입니다. 그러면 이제 수많은 집합들을 비교 할 수 있게 되었습니다!?

하지만 아직도 크기비교를 할 수 없는 더 많은 집합들이 존재합니다. 여러분도 예상 하셨듯, 문제가 되는 것은 무한집합(infinite set)의 경우였습니다. 예를들어 자연수(natural number) 집합 과 자연수 중 홀수(odd number)들의 집합 는 무엇이 더 크겠습니까?

갈릴레이(G. Galilei) 시대 까지는 무한집합에 관한 이와 같은 논의를 취급할 엄두조차 내지 못하였고, 칸토어(G. Cantor), 힐버트(D. Hilbert)에 와서야 논의가 정리되기 시작합니다. 결론부터 말하자면, 위와 같은 물음에 대해 '자연수 집합과 홀수 집합의 크기는 같다' 라고 정해지게 되었습니다.

일반적으로 집합 A와 B가 주어졌을 때, B가 A보다 크기가 크거나 같다는 것을 다음과 같이 정의합니다.

'일대일 함수 가 존재한다.'

아주 대충 말해서, 위에서 말하는 함수(functlon)(왜 이 알흠다운 단어가 오유에서 금지단어인가요? i대신 l 넣었습니다-_-;;;)란 집합 의 서로 다른 원소 전부를 집합 의 원소 하나를 짝지어주는 대응관계를 말합니다. 예를들어 , 일 경우, 는 함수가 됩니다. (각 순서쌍들(3개) 첫번째 좌표는 의 원소를 서로 다르게 하나씩 뽑고, 두번째 좌표는 의 원소를 하나씩 뽑아 짝을 지은 것입니다.) 주로 , , 라고 표기를 합니다. 이 때, 의 모든 원소가 순서쌍 첫번째 좌표에 등장해야만 한다는 사실에 주목하시기 바랍니다.

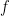
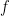
그렇다면 일대일(one-to-one)이라는 말은 무슨 뜻일까요? 이는 함수 에서, 순서쌍 두번째 좌표들 또한 첫번째 좌표와 마찬가지로 전부 서로 다를 때 붙이는 말입니다. 바로 위의 예 는 와 의 두번째 좌표가 로 같기 때문에 (함수이지만) 일대일 함수(혹은 단사함수(injection)라고도 부릅니다.)가 아닙니다. 다음과 같은 그림은 일대일 함수인 예와 일대일 함수가 아닌 예를 잘 보여줍니다.


Fig1. 일대일 함수인 예


Fig2. 일대일 함수가 아닌 예


위 그림에서도 간접적으로 알 수 있으나, 이 일대일 함수라는 것을 잘 음미해보면 유한집합 ,에 대하여 의 원소의 개수가 의 원소의 개수보다 많거나 같을 때에만 에서 로의 일대일 함수가 존재한 다는 것을 쉽게 알 수 있습니다. 무한집합의 원소를 일일이 셀 수는 없지만 함수는 정의할 수 있다는 사실과 유한집합에 대한 위와 같은 사실을 결합하면, 앞서 언급한 일대일 함수를 이용한 집합의 크기비교는 유한집합의 경우의 좋은 확장적 정의가 될 것 같아 보입니다.

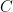
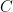
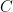
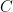
이제 따져봐야 할 것은 이러한 정의를 통해 '순서'라는 것을 정말 생각할 수 있느냐 하는 겁니다. 예를들어 집합 ,,에 대해 , 이면 인가? 그러니까, 에서 로의 일대일 함수가 있고 에서 로 일대일 함수가 있는데 에서 로의 일대일 함수가 없으면 어떻게 되는거-_-? 그러나 이러한 경우 항상 에서 로의 일대일 함수가 있다는 것을 증명할 수 있기 때문에 걱정하지 않아도 될 일입니다.

하지만 좀 더 큰 걱정이 있으니, 에서 로도 일대일 함수가 있고, 에서 로도 일대일 함수가 있으면 어떻게 되는건가 하는 물음입니다. 처음 크기비교를 정의할 때 단순히 '크다'가 아니라 '크거나 같다'에 대한 얘기를 하였으니, 양쪽으로 크거나 같으면 결국 같다는 얘기를 하고싶게 됩니다. 그러면 정말 크기가 '같을까?'

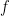
와 사이에 양쪽방향으로 일대일 함수가 있다면 둘 사이 일대일 대응(one-to-one correspondence)이 있음을 1896 ~ 1897년 번슈타인(F. Bernstein)과 슈레더(E. Schroder)가 독립적으로 증명하였습니다(Cantor–Bernstein–Schroeder theorem). 일대일 대응을 설명하기 위해 다시 집합 , 와 함수 를 생각해보도록 합시다. 앞서 일대일 함수를 설명할 때에는 순서쌍들의 두번째 좌표가 서로 다른지를 따졌는데, 이번에는 거기에다가 두번째 좌표에 의 원소 전부가 등장하는지를 따져볼 것입니다. 만약 전부 등장한다면, 그 함수를 전사함수(surjection)라고 합니다. 만약 일대일 함수이면서 전사함수이면 그 함수를 일대일 대응 혹은 전단사함수(bijection)이라고 합니다. 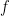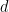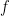물론 위의 함수 의 원소의 두번째 좌표에는 ,만 등장할 뿐 ,가 등장하지 않으므로 는 전사함수가 아닙니다. 저 위의 Fig2.는 일대일 함수는 아니지만 전사함수의 예가 됩니다.

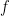
역시나 잠깐만 생각해보면, 유한집합의 경우 위와 같은 가 전사함수가 되려면 적어도 가 보다 커야한다는 사실을 쉽게 알 수 있을 것입니다. 다행히도 무한집합의 경우까지 고려 하더라도 에서 로의 일대일 함수가 존재하면 에서 로의 전사함수가 존재하는 것이 어렵지 않게 증명이 가능합니다.(단, 이것의 역 또한 참이지만 증명에 있어서 조금 어려운 개념을 익혀야합니다.) 다시말해 와 의 크기 비교에 있어서 일대일 함수를 통해 생각하여 가 보다 크기가 작다고 결론지었다면, 전사함수를 통해 생각할 때 가 보다 크기가 크다는, 결국 같은 결론을 준다는 이야기입니다.

다시 본론으로 돌아가서, 일대일 함수이면서 전사함수인 함수를 일대일 대응이라고 부르고, 위의 논의를 연장시켰을 때, 만약 와 사이에 일대일 대응이 존재한다면 와 의 크기가 같다는 얘기를 할 만 합니다. 물론 에서 로의 일대일 대응이 있으면 에서 로의 일대일 대응이 있는가 등의 조건을 따져줘야 우리가 "같다"는 용어를 써도 make sense할 것입니다. 따지는 것은 생략하고 중간 요약을 해보도록 하겠습니다.

1. 집합 ,에 대하여 가 보다 크거나 같다는 것은 일대일 함수 가 존재한다는 말이다.
2. 집합 ,에 대하여 와 의 크기가 같다는 것은 일대일 대응 가 존재한다는 말이다.


기나긴 사전준비가 끝났으니 이제 무한집합의 크기를 본격적으로 비교해봅시다.

우선 앞서 예로 든 자연수 집합과 홀수 집합의 경우 (단, ) 같은 순서쌍을 통해 일대일 대응을 만들 수 있음을 가볍게 알 수 있고(① 첫번째 좌표에 자연수 전부가 서로 다르게 등장하고(함수) ② 두번째 좌표에 홀수가 서로 다르게 등장하고(일대일 함수), ③ 두번째 좌표에 홀수가 전부 등장한다(전사함수)), 자연수 집합과 홀수 집합의 크기가 같다고 결론지을 수 있습니다. 마찬가지로 , 등을 통해 자연수 집합과 짝수(even numeber) 집합, 제곱수(square number) 집합 또한 크기가 전부 같음을 알 수 있습니다.

자연수 안에서만 놀기에는 지루하니까 이제 정수(integer)를 건드려봅시다. 자연수 집합과 정수 집합은 무엇이 더 많을까요? 다음과 같은 함수는 자연수 집합과 정수 집합 사이의 일대일 대응이 됩니다.



위를 식으로 쓸 수도 있으나 지저분해 보일 수 있기 때문에 몇개 나열하여 규칙을 보여드렸습니다. 첫번째 좌표는 자연수 1,2,3,... 을 따라가고, 두번째 좌표에는 0,1,-1,2,-2,3,-3,...과 같이 정수 집합의 모든 원소를 서로 다르게 나열시킵니다. 따라서 자연수 집합과 정수 집합의 크기는 같다고 할 수 있습니다.

이쯤에서 멀리서 가만히 내려다보면 자연수와 일대일 대응이 있는지 보기 위해서는 하나씩 하나씩 나열하여 전부 쓸수 있느냐가 관건인 것을 알 수 있습니다. 홀수는 1,3,5,7, ... 짝수는 2,4,6,8, ... 제곱수는 1,4,9,16, ... 정수는 0,1,-1,2,-2, ... 와 같이 차례대로 쓰면 전부 쓸 수 있음이 명백합니다. 이제 왼쪽부터 1,2,3,4, ... 하고 번호를 붙이면 그게 곧 자연수와의 일대일 대응이 되는 것입니다.

유리수를 한번 세어봅시다. 아래 그림에서 빨간색을 건너 뛰면서(!) 화살표를 따라 1,2,3,4,... 하고 번호를 붙이면 양의 유리수와 자연수와의 일대일 대응이 완성됩니다.(양의 유리수를 정말로 빠짐없이 세는 것에 주목하시기 바랍니다.)



이제, 양의 유리수와 자연수의 크기가 같으므로, 아까 정수와 자연수 사이의 일대일 대응을 생각 하듯이 음의 유리수까지 포함시킨 모든 유리수와 자연수 사이의 일대일 대응을 생각해낼 수 있을 것입니다. 즉, 유리수 집합 또한 자연수 집합과 크기가 같습니다. 이 사실은 꽤나 놀라운데, 수직선 위에 자연수, 정수는 띄엄띄엄 있어서 대략 개수가 비슷해 보이지만 유리수는 조밀(dense)한 만큼 훨씬 큰 집합처럼 보이는데 사실은 크기가 같기 때문입니다.

그러면 혹시 모든 무한집합의 크기는 자연수와 같지 않을까? 하는 물음이 솟구쳐 오를 것입니다. 그러면 애초에 이 주제가 재미가 없으니 글을 써내려가지도 않았겠습니다-_-; 칸토어는 마침내 굉장히 흥미로운 발견을 하게 되는데, 실수 집합은 자연수 집합보다 크다(크거나 같다가 아님)는 사실이 바로 그것입니다. 증명이 유명하여 '칸토어의 대각법(Cantor's diagonal argument)'라는 이름까지 붙어있을 정도입니다. 증명의 개요는 다음과 같습니다. '①실수 집합은 자연수 집합보다 크거나 같다. ②그런데 실수 집합이 자연수 집합과 크기가 같다고 치면 모순이 발생하므로, ③실수 집합은 자연수 집합보다 크다.'

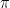
우선 이라는 순서쌍을 통해 자연수로부터 실수로 가는 일대일 함수가 있음은 매우 쉬운 사실이고, 따라서 ①은 바로 해결됩니다. 문제는 ②인데, 증명에는 10진법 표기를 이용합니다 : 임의의 실수는 10진법 표기를 할 수 있다는 사실을 받아들입시다. 예를들어 는 3.141592 ... 입니다. 이제 모든 실수를 10진법 표기 하고 자연수에 일대일 대응시켰다고 합시다. 그 모든 실수 중, 0과 1 사이에 있는 실수를 전부 뽑아봅시다. 그것들은 각각 어떤 자연수와 짝을 이룰 것인데, 자연수 짝꿍 중에 가장 작은 것들부터 순서 쌍을 차례로 적을 수 있고, 일반적으로 다음과 같은 꼴일 것입니다.









(단, ...)

이 때 두번째 좌표에 있는 0,1사이의 실수들만 순서를 유지하여 나열해보면 다음과 같겠지요.









여기서 다음과 같은 수을 생각해봅시다.



이 수는 위의 실수 리스트에서 대각성분만 뽑아 구성한 실수로서, 0과 1 사이의 실수가 됩니다. 이제 다음과 같은 새로운 실수를 생각해봅시다.






이 수 또한 정수부분이 0이므로 0과 1 사이의 실수임이 분명한데,,, ?! 만약 이 수가 위에서 번째 리스트에 있다면, 소수 번째 자리에서 이어야 하고 모순이 발생합니다!
(이 증명에서 9가 연속적으로 나타나는 등의 세부적 문제점은 논외로 하였습니다.)

이로서 실수가 자연수보다 크기가 더 크다는게 증명되었습니다. 다시말해 실수와 유리수는 수직선 상에서 둘 다 조밀히 채워져있지만, 크기가 같지 않으며 유리수가 실수보다 크기가 작습니다. 사실 유리수는 실수보다 크기가 한참작은데, 실수에서 유리수를 뺀 무리수 집합이 실수 집합과 크기가 같기 때문입니다(즉 유리수 집합이 실수 집합 크기에 비해 전혀 영향성이 없습니다.).

살짝 힘들지만 조금 더 나아가 봅시다. 더 궁금한 것은 실수 집합보다 큰 집합이 있느냐는 것입니다. 칸토어는 직관적으로 좌표평면이 실수직선보다 차원이 더 큰 만큼, 크기도 좌표평면 집합이 실수 집합보다 크다고 생각하였으나, 실제로는 같다는 것을 증명합니다(이에 대해 본인이 증명해놓고도 믿기 힘들다 했다고 하니... 그만큼 선 위의 점들과 면 위의 점들의 개수가 같다는게 많이 쑈킹하죠. 증명은 어렵지 않으나 이 얘기를 구체적으로 시작하면 또 할 얘기들이 많아질 것 같아서 생략합니다;). 물론 나아가, 공간좌표계 및 임의의 유클리드 공간 이 실수와 크기가 같다는 것도 보여집니다. 그러면 실수보다 더 큰 집합이 정말 없을까요? 여기서 다음과 같은 쉬운 개념 하나를 알고 넘어갈 필요가 있겠습니다.

는 의 멱집합(power set)(멱이라는 한문이 정확히 무엇을 뜻하는지 모르겠습니다;;)을 의미합니다. 멱집합이란 부분집합(subset) 전부를 원소로 하는 집합인데, 다음과 같은 예를 보면 이해가 쉬울 것입니다.



(단, 는 공집합(empty set))

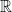
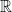
칸토어는 의 크기가 의 크기보다 크다는 사실을 증명할 수 있었습니다(Cantor's theorem). 즉, 실수집합 에 대해 은 보다 크기가 크고, 은 그보다 더 크고, ... 이와 같이 더 큰 집합을 계속 만들어 나갈 수 있었습니다. 증명은 칸토어 대각법과 흡사한 방법으로 진행됩니다 : ①집합 는 집합 보다 크거나 같다. ②그런데 가 와 크기가 같다고 치면 모순이 발생하므로, ③은 보다 크다.

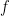
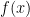
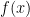
의 모든 원소 에 대해, 의 원소 중 가 있으므로 순서쌍 는 에서 로 가는 일대일 함수를 줍니다. 즉 는 보다 크거나 같습니다. 이제 일대일 대응 가 있다고 합시다. 그러면 다음과 같은 집합 (즉 의 원소 들 중 안에 들어가지 않는 것들만 모은 것. 가 의 원소이므로 의 부분집합임에 주의하세요.)를 생각할 때 는 의 부분집합이므로 의 원소인데, 그러면 가 일대일 대응이므로 어떤 의 원소 에 대해 , 즉 이어야 할 것입니다. 이 때 는 에 들어가거나, 들어가지 않거나 둘중 하나일텐데, 가 만약 의 원소이면 집합 의 구성에 의해 는 안에 없어야 하므로 인 것에 모순이고, 가 의 원소가 아니면 마찬가지로 집합 의 구성에 의해 는 안에 있어야 하므로 또한 인 것에 모순입니다.

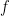
결국 가 에 들어가도 모순이고 들어가지 않아도 모순이니 뭔가 처음부터 잘못되었음을 의미합니다. 즉, 이러한 일대일 대응 는 애초에 없어야 마땅한 것입니다. 사실 이 방법은 칸토어 대각법과 흡사하디 못해 거의 완벽하게 같은 방법인데 이에 대한 논의는 제외하겠습니다.

이제 이 Cantor's theorem에 의해 우리는 어떤 집합 가 주어지면 그것보다 크기가 큰 집합 를 창조해 낼 수 있게되었습니다. 라고 두기만 하면 됩니다. 잠시 이 정리의 흥미로운 응용을 보도록 하겠습니다. 수학적 objects 전체의 집합, 즉 우리가 생각할 수 있는 가장 큰 집합을 라고 합시다. 그러면 는 보다 크기가 크므로 가 가장 크다는 것에 모순입니다? 어디가 잘못되었을까요?? 사실, 이로부터 우리는 '가장 큰 집합이라는건 없다.'라고 결론 지을 수 있습니다. 가장 큰 집합의 존재성은 여러 방법으로 부정될 수 있는데, 위의 Cantor's theorem도 그 방법들 중 하나가 될 수 있습니다.

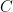잠시 숨을 고르고, 이로부터 또 다른 궁금한 점을 알아보겠습니다. 크기를 계속 키울 수 있다는 것은 알겠다. 그러면 집합 와 가 있고 가 보다 크기가 클 때, 의 크기와 의 크기 사이의 크기를 가지는 집합 가 존재하는가? 이에 관해서는 집합론을 섬세하게 파고들어야 비교적 만족할만한 답변을 얻을 수 있어 자세한 설명은 생략하...겠습니다.

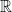
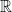
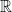
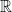
간략하게라도 말하면, 우선 자연수 집합 은 무한집합 중 가장 작은 집합이며, 그보다 바로 큰 집합 이 존재하고 그것을 수학적으로 잘 정의할 수 있습니다. 여기서 바로 큰 집합이라는 것은, 과 사이의 크기를 가지는 어떠한 집합도 없다는 이야기 입니다('크기'라는게 이렇게 띄엄띄엄하게 있다는 것도 상당히 신기한 사실로 다가옵니다만...). 그런데 한편, 실수집합 이나, 은 보다 크기가 크다는 것을 앞에서 알아보았습니다. 문제는 얘네가 얼마나 큰가인데, 과 은 크기가 같다는 것이 이진법을 이용하여 비교적 쉽게 해결이 되나, 과 의 크기 비교는 간단치 않은 문제가 됩니다. 이것을 해결하기 위해 칸토어는 정신병까지 앓으며 평생을 고생하였지만 헛수고였습니다. 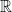수학자들은 의 부분집합 중, 열린집합(open set) 또는 닫힌집합(closed set), 나아가 Borel set이기만 하면 과 사이의 크기를 가질 수 없다는 것을 밝혀냈지만(open, closed, Borel같은 용어는 몰라도 됩니다. 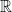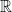중요한 것은 우리가 생각할 수 있는 실수의 많은 부분집합들이 과 사이의 크기를 가질 수 없다는 게 밝혀졌다는 것입니다.) 결정적으로 과 의 크기 비교에 도움이 되지 않았습니다. 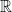악착같이 실수를 파고들어 cofinality라는 것을 정의하면서까지 과 사이의 집합을 찾으려고 하였으나 를 밝혀낼 수 있을 뿐, 두번째 부등호의 등호를 뺄 수가 없었습니다.

마침내 괴델(K.Godel)과 코헨(P.Cohen)이 기존 집합론 체계에서 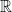과 의 크기 비교를 할 수 없음을 증명하였습니다(?). 크거나 작거나 같거나 셋중 하나지 비교할 수 없다는건 뭔소린지 아리송하실 수 있는데, 사실이 그렇습니다-_-a 이에 관해서 다음에 쓸 기회가 있으면 몇자 적어보겠습니다.




===============================

오랜만에 텍언어를 쓰니 시간이 꽤 걸리네요 ㅠ_ㅠ

이런 삭막한 내용으로 베스트는 무리려나...