본 프로젝트는 포커를 칠 때, 내 카드와 상대방의 공개된 카드를 보고 Raise를 선택할지 Check를 선택할지 Call을 선택할지 혹은 Fold를 선택해야할지 판단해주는 프로그램을 만들어보려고 시도하였다.
포커는 52장의 카드로 이루어진 Deck에서 카드를 3장씩 뽑은 뒤에 각자 1장의 카드를 공개하고, 공개한 카드로 선플레이어를 나눈 뒤 선플레이어부터 Check/Raise를 선택하거나 혹은 Fold를 선택한다, 그 후 후 플레이어는 그 선택에 따라 각각 Raise, Check, Call, Fold를 선택하고, Chack/Call로 판돈이 합의가 되면 다음 패를 받아 공개된다. 여기서 부터 세븐포커와 파이브포커가 나뉘는데, 가짓수를 낮추기 위해서 파이브포커를 선택한다. 만일 마지막패(상대방 패는 비공개)를 받을때까지 서로 Fold한 사람이 없다면 각자의 패의 족보를 겨루어서 승자가 모든 판돈을 가져간다.
여기서 포커플레이어가 알 수 있는 정보는 1. 나의 패(받은 패), 2. 상대방의 패(공개된 패) 3. 상대의 방금 선택(Raise, Check, Call, Folde), 4. 현재 판돈이다. 1~3번 정보는 갯수를 셀수 있는 유한 집합이지만, 4번같은 경우에는 사실상 무한 집합이다. 부득이하게 무한 집합에 대한 판단 가치를 두는 것은 가짓수를 무한히 증가 시키는 계기가 되므로 프로그램에서는 의도적으로 무시하도록 한다.
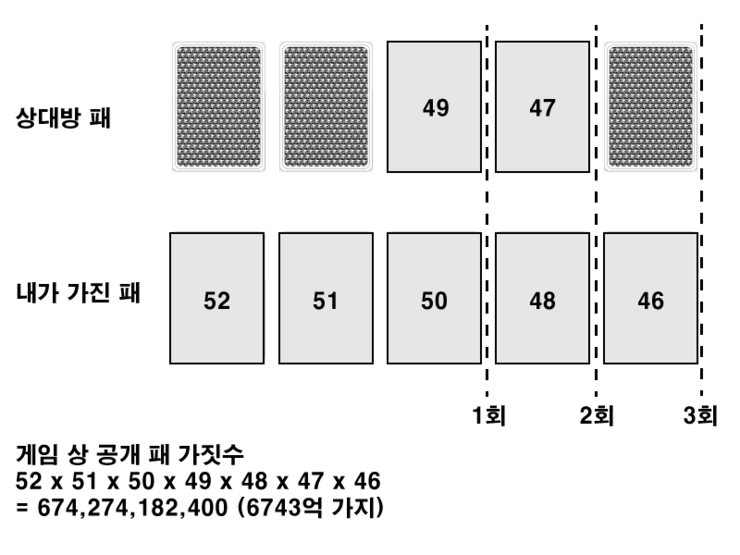
이 때 계산해볼 수 있는 가짓수는 약 6743억 가지이다. 하지만 문제는 48, 47, 46으로 가짓수 판단된 카드는 1회차 2회차 배팅에서는 모르는 카드로 판단되어짐이 마땅하다. 따라서 각 가짓수에 +1(모른다)가 포함되어야 한다.
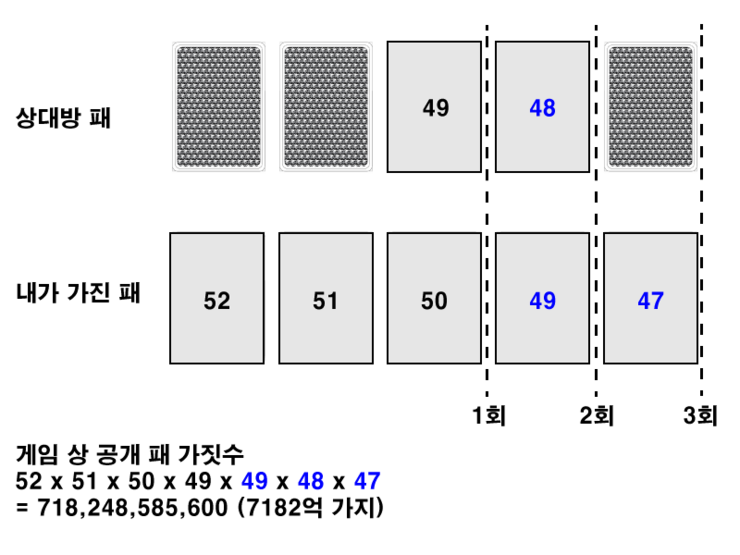
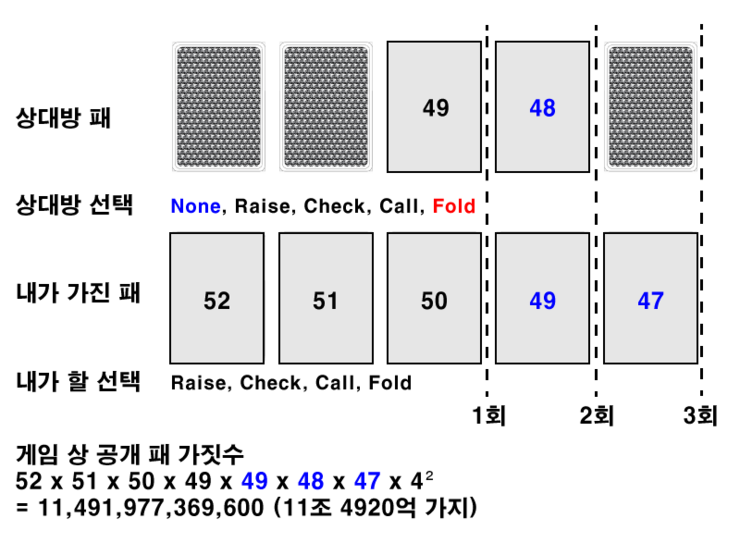
그리고 마지막으로 상대방의 방금 선택을 포함시켜야한다. 그 중 내가 선플레이어였을 때 상대방의 선택이 없을 때를 포함하고 상대가 Fold를 선택하면 내 선택이 필요없이 승리하므로 4가짓수라고 판단한다, 또한 나의 선택 포함되어야 한다.
이제부터 무한한 포커 게임을 시행하면서 데이터를 축적해 나간다. 알고리즘은 다음과 같이 진행한다.
1. 덱을 셔플 후 카드를 10장 추려낸다
2. 각 선수에게 1, 2, 3번째 카드를 보여주고 상대에게 공개할 카드를 선택한다. (#상황 1을 로그에 추가)
3, 공개카드의 족보대로 선 플레이어부터 Raise, Check, Call, Fold를 선택하여 게임을 진행한다. (#상황 n을 로그에 추가)
3-1. Fold를 선택한 경우 or 마지막 카드 공개 후 판돈이 합의된 경우 4로 진행
3-2. 그 외 순서대로 3번 진행
4. 게임 종료와 함께 각 선수의 이득을 계산하고 데이터에 축적 (목표 데이터 N개를 충족할 때까지 1번 진행)
(상황 1, 이득/손실)
(상황 2, 이득/손실)
... → 1차 저장소에 기록
(상황 n, 이득/손실)
5. 1차 저장소에 있는 내용들을 Main 저장소에 업데이트
이전 Main 저장소 1차 저장소 신규 Main 저장소
(상황 1, 평균 기대이익, 표본 수) (상황 1, 평균 기대이익, 표본 수) (태그1, 갱신 기대이익, 표본 수x 2)
(상황 2, 평균 기대이익, 표본 수) (상황 2, 평균 기대이익, 표본 수) (태그2, 갱신 기대이익, 표본 수x 2)
... + →
(상황 n, 평균 기대이익, 표본 수) (상황 n, 평균 기대이익, 표본 수) (태그 n, 갱신 기대이익, 표본 수x 2)
6. N을 두배로 늘리고 1번 진행
그렇다면 이제 포커를 치는 함수를 제작해야한다. 각 카드를 어떻게 정의하는가 부터 시작한다.

※ 0번은 모르는 카드를 표현한다(비공개 or 오픈되지 않은 카드)
족보 순서대로 무식하게 때려박았다. 그로인해 단일 카드 족보 찾기는 수월해졌다. (고유 숫자가 낮은 쪽이 높은 카드), 다음은 카드 조합으로 만들어지는 족보들을 판단할 차례이다.
노페어 : 가진 카드 중 가장 낮은 고유 숫자를 노페어 대표 카드로 선정한다.
원페어 : A~K까지 갯수를 세어 2장 있다면 원페어, 해당 카드 중 가장 낮은 고유 숫자를 원페어 대표카드로 선정한다.
투페어 : A~K까지 갯수를 세어 2장, 2세트 있다면 투페어, 해당 카드 중 가장 낮은 고유 숫자를 투페어 대표카드로 선정한다.
트리플 : A~K까지 갯수를 세어 3장 있다면 트리플, 해당 카드 중 가장 낮은 고유 숫자를 트리플 대표카드로 선정한다.
스트레이트 : 카드 번호 낮은 순으로 정렬하여 첫째 + 4 = 둘째 + 3 = 셋째 + 2 = 넷째 + 1 = 다섯째일때 스트레이트, 다섯째 카드를 대표카드 로 선정한다. (마운틴을 포함한다)
백스트레이트 : 카드번호가 1, 10, 11, 12, 13일 때, 스트레이트 판정, 숫자가 10인 카드가 대표 카드로 선정
※ 한국 포커 룰에서는 백스트레이트를 마운틴 다음가는 족보로 생각하지만 영미권 포커 룰에서는 백스트레이트를 최하급 스트레이트 족보로 선정하며 프로그래밍 하는 입장에서 보아도 최하급으로 계산하는게 원래 포커룰에 더 합치하는 것으로 보이므로 에이스가 대표가 되지 않고 최하급 대표카드가 대표로 선정됨
플러시 : 모든 카드가 같은 문양으로 판정되면 플러시, 가장 낮은 숫자(노페어 대표카드)가 대표 카드로 선정
풀하우스 : 트리플과 투페어가 모두 선언되었을 때 풀하우스, 트리플 대표카드가 풀하우스 대표 카드로 선정
포카드 : A~K까지 갯수를 세어 4장 있다면 포카드, 스페이드 카드가 대표 카드로 선정
스트레이트 플러시 : 스트레이트와 플러시가 모두 선언되었을 때 스트레이트 플러시, 스트레이트 대표 카드가 스티플 대표 카드로 선정
(로얄 스트레이트 플러시를 포함한다)
이 함수가 제대로 작동하는지 파악하는 방법은 계속 포커를 치게 만든 후 나온 족보를 확률 계산과 비교해보는 방법이 있다.
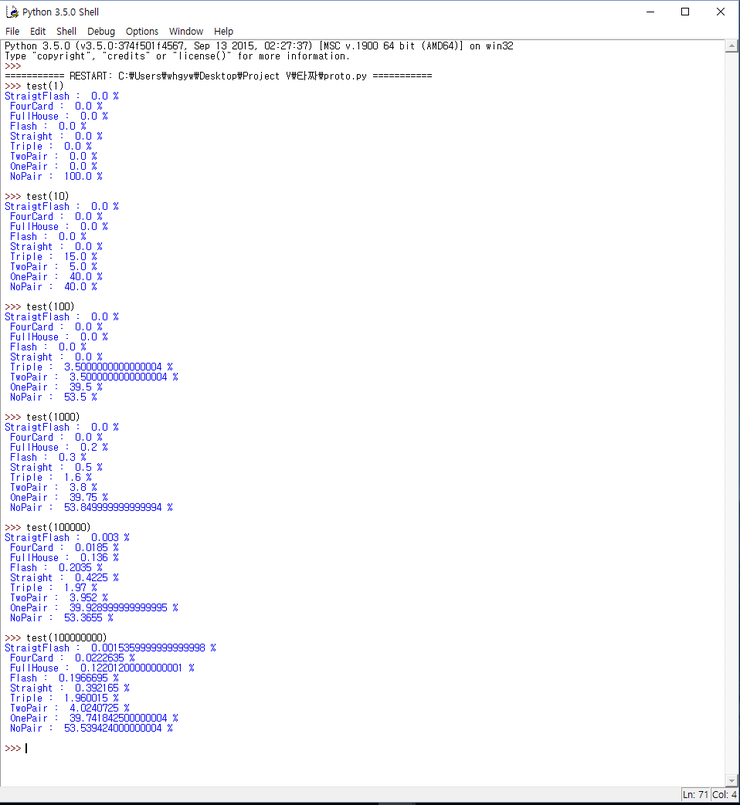
※마지막 1억번 포커치는 건 2.7시간 걸렸다!
http://cafe.naver.com/daeryunsaemter/45
교사 박준혁님이 올려주신 포스트와 표본으로 등장한 확률을 비교해보자. 몇가지 차이는 나지만 어느정도 비슷하니 그럴듯하게 완성됬다고 판단하자.
여기서 포커 프로그램 만들기에 대한 생각이 접혔다. 이유는 포커 판 1억판 (사실상 2억판 A, B 두 사람이 치는 포커 1억판으로 계산했기 때문에..)을 치는데 2.7시간이 걸렸다면, 통계학적으로 모든 데이터가 1번씩 적립되려면 11조 5천억 판을 쳐야한다. 그렇다면 2억판 데이터 적립에 2.7시간으로 대충 계산해봐도 155,141.7 시간이 걸린다. 햇수로 세자면 17.7년 정도 걸린다는 셈이다. 데이터가 누적되어 평균값을 계산해야하기에도 모자란 시간에 모두 돌리는데 17.7년이 걸린다면 안하는게 낫다라고 판단되어진다..
본인 컴퓨터의 CPU 점유율로 생각해도 4개 병행하여 돌리는게 최상이라고 생각되는데 그렇다면 4.5년에 1번 사이클이 돈다. 그리고 알파고에 사용되었다는 CPU 1202개를 사용한다면 (각 CPU당 4개씩 병행한다면) 32.26시간에 1사이클이 돈다.
하지만 나는 1202개의 컴퓨터가 없다. 그래서 여기서 멈춘다. 다음 프로젝트는 러닝 머신에 대한 것으로 잡을까 생각중이다.

















